Phénomène binaire |
1° Définition
Il est fréquent qu’un phénomène se traduise par l’existence de deux états différents et deux seulement.
Un tel phénomène est dit binaire.
Ainsi :
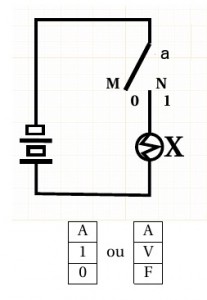
— un circuit électrique ne peut être qu’ouvert ou fermé ;
— en logique mathématique, on ne considère, parmi les phrases ayant une signification, que celles dont on s’accorde à reconnaître qu’elles sont soit vraies, soit fausses. De telles phrases sont appelées propositions.
 |
Par exemple : « Paris est la capitale de la France » est une proposition (vraie) ; «  » est une proposition (fausse) ; « Si je dis : je mens, est-ce que je mens ? » n’est pas une proposition. |
— en mathématiques, un ensemble est défini lorsque, pour tout objet, on peut répondre par « oui » ou par « non » à la question : « Cet objet fait-il partie de l’ensemble ? ». De même, une propriété mathématique est soit vraie, soit fausse.
Ainsi, par exemple, on peut parler de :
– l’ensemble des lettres a, b, c et d. On note 
cet ensemble ;
– l’ensemble des nombres entiers pairs. ; on ne peut pas parler de « l’ensemble des personnes intelligentes » car … chacun voudrait faire partie de cet ensemble et, cependant, chacun reconnaît qu’il y a partout des… imbéciles !
— dans la numération binaire, les seuls chiffres utilisés sont le 0 et le 1. Par suite, dans l’écriture d’un nombre entier, la suite des chiffres ne contient que des 0 ou des 1 (voir système binaire). Exemples :
- zéro sera noté 0 ; un sera noté 1 ;
- deux est formé d’ une paire et de zéro unité ; il est noté 10 (lire « un, zéro ») ;
- trois est formé d’une paire et de une unité ; il est noté 11 (lire « un, un ») ;
- quatre est formé d’une « paire de paires », zéro paire, zéro unité ; il est donc noté 100 (lire « un, zéro, zéro » ) ;
- cinq est formé d’une « paire de paires », zéro paire, une unité ; « il est donc noté 101 (lire « un, zéro, un »).
- Alors : six est noté 110 ; sept : 111 ; huit : 1000 ; neuf : 1001 ; dix : 1010 ; onze : 1011 ; etc.
2° Représentations d’un phénomène binaire Soit A un phénomène binaire. Puisque A ne prend que deux états s’excluant mutuellement (soit vrai, soit faux) , on affecte à l’un des états la valeur 0 (en général, à la fausseté), à l’autre état la valeur 1 (en général, à la vérité).
— pour un montage électrique : Dans cette figure, M et N sont les deux bornes d’un circuit électrique. Le contact — noté  — si A est le phénomène qu’il « représente » est ouvert au repos (le courant ne passe donc pas et la lampe X reste éteinte) et, dans cette position, il correspond à l’état 1 du phénomène A. Lorsque l’on actionne le contact  , alors le courant passe et, dans cette position, le contact correspond à l’état 1 du phénomène A et la lampe X s’allume. Il importe de remarquer que, dans les représentations des montages électriques, tous les contacts sont considérés à l’état de repos, c’est-à-dire non actionnés.– en logique, on dresse la table de valeur, ou de vérité, de chaque proposition, de la façon ci-contre pour la proposition A. |
 (V pour vrai ; F pour faux). |
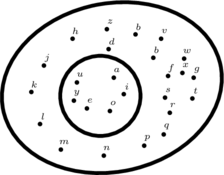
— en mathématiques, on schématise les ensembles que l’on considère de l’une ou l’autre des manières ci-dessous. (Nous avons schématisé l’ ensemble des lettres de l’alphabet français).
| Lettres de l’alphabet | |||||||||||||
|
|
|
||||||||||||
| Diagramme de Carrol | Diagramme d’Euler-Venn |
