Savoir dire « NON » |
En logique
Soit la proposition 
: « demain, j’irai au cinéma ». Il est possible de considérer la nouvelle proposition, notée 
(lire « A barre » ou « non A ») suivante : « demain, je n’irai pas au cinéma ». Cette nouvelle proposition, appelée négation de est : vraie quand est fausse et est fausse si est vraie. Autrement dit, les tables de vérité (ou de valeurs) des propositions et sont :
|
|
Ce résultat est valable, plus généralement, quelle que soit la proposition considérée.
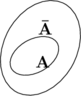
En théorie des ensembles, dès que l’on considère une partie d’un ensemble (par exemple, les voyelles de l’alphabet français), on définit par cela même une autre partie (appelée complémentaire de la précédente [ par exemple, les non voyelles (ou consonnes) ]. Si la première partie rend vraie une certaine propriété (ou proposition ), alors la partie complémentaire rend vraie la proposition . On schématise cela de l’une des façons suivantes (en désignant par la partie complémentaire de la partie ).
|
|
Montage électrique.
Il suffit que l’interrupteur, à l’état de repos soit sur la position 1, lorsque est vraie. Alors, en agissant sur lui, il passera sur la position 0. Autrement dit, la lampe  est éteinte quand est vraie, allumée quand est faux. Ce montage réalise donc la négation de .
|
 |
Phénomène binaire
Soit le phénomène : « éclairage public des rues ». Affectons la valeur 0 à l’absence d’éclairage artificiel et la valeur 1 au cas contraire. Soit le phénomène « éclairage naturel » prenant la valeur 1 si cet éclairage est jugé suffisant, la valeur 0 dans le contraire.
Il est immédiat que l’éclairage public doit prendre la valeur 1 si prend la valeur 0 et la valeur 0 si prend la valeur 1. Donc représente le phénomène « éclairage public ».