Savoir dire « ET » |
- En logique : conjonction de deux propositions ou produit logique.
Soit la phrase : « demain j’irai au cinéma et j’irai voir l’ami Pierre ».
Si l’on considère les deux propositions :
A : « demain j’irai au cinéma » ; B : « demain j’irai voir l’ami Pierre » ; La phrase proposée s’écrit A et B. Chacun s’accordera à reconnaître qu’elle n’est vraie que si les deux propositions A, B sont simultanément vraies (un cas) ; fausse si l’une au moins des deux propositions est fausse (trois cas : A fausse et B vraie ; A fausse et B fausse ; A vraie et B fausse)
On dit que A et B, notée A et B ou A
B ou A 
B ou enfin AB , est la conjonction (ou le produit ) logique des propositions A et B.
La table de valeur ou de vérité de AB est :A B AB F F F F V F V F F V V V A B AB 0 0 0 0 1 0 1 0 0 1 1 1 La table de valeur ci-dessus justifie l’expression « produit logique » puisque :
; 
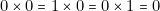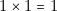et, par suite la notation A B est couramment employée, de même que AB comme en algèbre classique. - En théorie des ensembles.
Soit E l’ensemble des lettres du mot « beau » et F l’ensemble des lettres du mot « bahut ». Ces deux ensembles ont en commun les éléments « a, u, b ». On dit que l’ensemble « a, u, b » est l’intersection des ensembles E et F. Ces éléments sont ceux qui appartiennent à la fois à E et à F.
Plus généralement, si
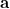est l’ensemble des éléments rendant vraie une proposition A, si 
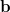est celui rendant vraie une proposition B, l’intersection de 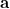et 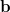, notée 
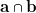(lire « a inter b »), rend vraie la proposition AB (produit logique de A et B). On représente cela de l’une des manières suivantes :
a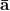 
b a ∩ b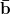 
• Circuits électriques. Pour que la lampe X s’allume, il faut et il suffit que les deux interrupteurs, lorsqu’on agit sur eux, soient simultanément sur la position 1 (figure ci-contre, ne pas oublier que les schémas sont représentés à l’état de repos). Autrement dit, le circuit « montage en série », correspond au produit logique. 
X = AB