Savoir dire « OU » |
Remarquons d’abord que, dans le langage courant français, la conjonction « ou » est ambiguë. Par exemple :
- — « fromage » ou « dessert » portent, parfois, les menus des restaurants. Il faut alors comprendre que c’est soit l’un, soit l’autre, à l’exclusion des deux.
- — « tarif réduit aux étudiants ou aux adhérents du ciné-club » ; là il faut comprendre que l’étudiant adhérent du ciné-club a aussi droit au tarif réduit.
Dans le premier cas, le « ou » est dit exclusif ; dans le second cas, il est dit « non exclusif ».
Remarquons aussi qu’en anglais, les deux sens du mot « ou » sont distingués : « or » ayant le sens non exclusif ; « either…, either… » le sens exclusif. Il en est de même en allemand « oder », sens non exclusif ; « entweder…, oder… », sens exclusif. De même en latin : « aut », ou exclusif ; « vel », sens non exclusif.
Le « ou » considéré par la suite sera non exclusif.
- En logique.
- — Soit la phrase : « demain j’irai au cinéma ou j’irai voir l’ami Pierre »}.
Si l’on considère les deux propositions :
A : « demain j’irai au cinéma » ; B : « demain j’irai voir l’ami Pierre » ; La phrase considérée s’écrit alors A ou B. On dit que c’est la conjonction logique des propositions A et B. On s’accordera à dire que A ou B est : vraie si, au moins l’une des propositions A et B est vraie (trois cas) ; fausse si A et B sont simultanément fausses.
- — Plus généralement, étant données deux propositions A, B, la conjonction A ou B, notée
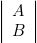 , admet les tables de valeur (ou de vérité) ci-dessous :
, admet les tables de valeur (ou de vérité) ci-dessous :
A B 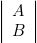
F F F F V V V F V V V V A B 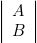
0 0 0 0 1 1 1 0 1 1 1 1 Remarque importante.
La conjonction logique
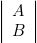 , aussi nommée produel, est souvent notée, non sans danger,
, aussi nommée produel, est souvent notée, non sans danger,  (autrefois, appelée somme logique des propositions
(autrefois, appelée somme logique des propositions 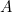 et
et 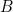 ).
). - Les règles d’utilisation de cet opérateur sont :
 (première ligne)
(première ligne)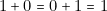 (2
(2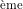 et 3
et 3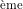 lignes)
lignes)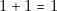 (4
(4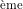 ligne).
ligne).Dans ce livret d’initiation, afin d’éviter toute erreur chez les débutants,nous noterons la conjonction logique «
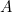 ou
ou 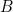 ». La disposition verticale, d’une part, évite la confusion avec l’opérateur
». La disposition verticale, d’une part, évite la confusion avec l’opérateur 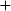 et traduit, d’autre part, la disposition du montage parallèle.
et traduit, d’autre part, la disposition du montage parallèle.
- — Soit la phrase : « demain j’irai au cinéma ou j’irai voir l’ami Pierre »}.
Si l’on considère les deux propositions :
- En théorie des ensembles.
- — Soit E l’ensemble des lettres du mot « beau » et F l’ensemble des lettres du mot « bahut ». L’ensemble des lettres entrant dans l’écriture du mot « beau » ou du mot « bahut » est la réunion des ensembles E et F . On note E
 F ( lire « E union (ou réunion) F ) cet ensemble. Ici : E
F ( lire « E union (ou réunion) F ) cet ensemble. Ici : E  F =
F = 
- — Plus généralement,
soit a l’ensemble des éléments rendant vraie une proposition A,
soit b l’ensemble des éléments rendant vraie une proposition B,
la réunion
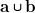 est l’ensemble des éléments rendant vraie la conjonction logique
est l’ensemble des éléments rendant vraie la conjonction logique 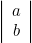 .
.
Ceci se représente de l’une des façons suivantes :
a 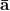
b a ∪ b 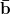
• Circuits électriques.
Pour que la lampe X s’allume il faut, et il suffit, que l’un au moins des interrupteurs A ou B soit, quand on agit sur eux, sur la position 1 (figure ci-contre, les interrupteurs sont à l’état de repos). Autrement dit, le « montage en parallèle » correspond à la conjonction logique.
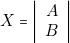
- — Soit E l’ensemble des lettres du mot « beau » et F l’ensemble des lettres du mot « bahut ». L’ensemble des lettres entrant dans l’écriture du mot « beau » ou du mot « bahut » est la réunion des ensembles E et F . On note E
