Notice 2Le logicien, les saints et les menteurs |
Le logicien, les saints et les menteurs
- 1° Analyse du problème.
- Les lampes
 ,
, 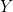 ,
, 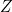 allumées (resp. éteintes) indiquent que la 1
allumées (resp. éteintes) indiquent que la 1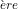 personne interrogée, la 2
personne interrogée, la 2 , la 3
, la 3 sont des saints (resp. des menteurs). La clé du problème tient au fait que le logicien connait la réponse donnée par la 1
sont des saints (resp. des menteurs). La clé du problème tient au fait que le logicien connait la réponse donnée par la 1 personne sans qu’il soit nécessaire de comprendre celle-ci. En effet : si cette personne est un saint elle dit « je suis un saint » ; si cette personne est un menteur, elle… ment et elle dit « je suis un saint ».
Autrement dit, la première personne répond toujours « je suis un saint ».
personne sans qu’il soit nécessaire de comprendre celle-ci. En effet : si cette personne est un saint elle dit « je suis un saint » ; si cette personne est un menteur, elle… ment et elle dit « je suis un saint ».
Autrement dit, la première personne répond toujours « je suis un saint ».
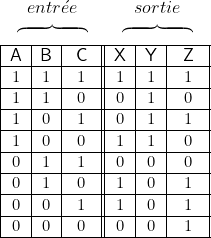
Ceci conduit à la Table de valeurs ci-dessus. En effet :
- Table de valeurs.
- — Si, par exemple, la 2
 personne interrogée répond « le 1
personne interrogée répond « le 1 a dit qu’il est un menteur » on inscrit
a dit qu’il est un menteur » on inscrit 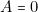 , mais on sait qu’alors cette deuxième personne ment, donc
, mais on sait qu’alors cette deuxième personne ment, donc 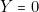 , ce qui permet de remplir de 0 les quatre dernières lignes de la colonne
, ce qui permet de remplir de 0 les quatre dernières lignes de la colonne 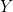 ;
; - — si, ensuite, la 3
 personne interrogée répond « le 1
personne interrogée répond « le 1 est un menteur » (c’est-à-dire
est un menteur » (c’est-à-dire 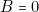 ) et « le deuxième est un menteur » (c’est-à-dire
) et « le deuxième est un menteur » (c’est-à-dire 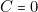 ), cette dernière phrase comparée au renseignement connu (la 2
), cette dernière phrase comparée au renseignement connu (la 2 personne est effectivement un menteur) assure que cette 3
personne est effectivement un menteur) assure que cette 3 personne est un saint (donc
personne est un saint (donc 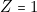 ) et, par suite, ce qui est vrai, « la 1
) et, par suite, ce qui est vrai, « la 1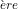 est un menteur » (
est un menteur » ( 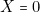 ). Ceci nous permet de remplir la dernière ligne de la table.
). Ceci nous permet de remplir la dernière ligne de la table. - — On procède de même pour les huit lignes. Ainsi pour
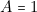 ,
, 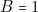 ,
, 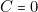 (2
(2 ligne).
ligne).
- 3° Expressions algébriques.
- — La lampe
 doit être allumée (
doit être allumée (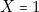 ) sur les « lignes» 1, 4 , 6, 7 correspondant à :
) sur les « lignes» 1, 4 , 6, 7 correspondant à :
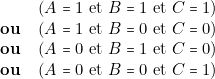 c’est-à-dire :
c’est-à-dire : 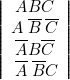
- — De même (lignes 1, 2, 3, 4 de la table) :

- — De même (lignes 1, 3, 6, 8 de la table) :
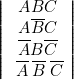
Donc
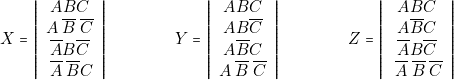
- — La lampe
- 4° Simplifications (voir 1
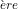 partie, § 6 et 8).
partie, § 6 et 8). ne peut être simplifiée. Donc :
ne peut être simplifiée. Donc :
![Rendered by QuickLaTeX.com \[ X=\left|\begin{array}{c} ABC\\ A\;\overline{B}\;\overline{C}\\ \overline{A}B\overline{C}\\ \;\overline{A}\;\overline{B}C \end{array}\right| \qquad \qquad Y=\left|\begin{array}{c} ABC\\ AB\overline{C}\\ A\overline{B}C\\ A\;\overline{B}\;\overline{C} \end{array}\right|= A\left|\begin{array}{c} B\\ \overline{B} \end{array}\right|=A \qquad \qquad Z=\left|\begin{array}{c} ABC\\ A\overline{B}C\\ \overline{A}B\overline{C}\\ \;\overline{A}\;\overline{B}\;\overline{C} \end{array}\right|=\left|\begin{array}{c} AC\\ \;\overline{A}\;\overline{C} \end{array}\right| \]](https://jr01.dhenin.fr/wp-content/ql-cache/quicklatex.com-26fac0d92ee7a693178a962377c65088_l3.png)
- 5° Schéma du programme (voir notice
 ).
).
- — Pour « alimenter » la lampe
 , il est nécessaire (puisqu’il y a quatre ou) de la relier à quatre « colonnes de programmation ». Nous avons choisi les colonnes 1, 2, 3, 4.Sur la colonne 1, nous avons mis
, il est nécessaire (puisqu’il y a quatre ou) de la relier à quatre « colonnes de programmation ». Nous avons choisi les colonnes 1, 2, 3, 4.Sur la colonne 1, nous avons mis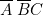 (fiches à droite sur les barrettes A et B, fiche à gauche sur la barrette C). Sur la colonne 2, nous avons mis
(fiches à droite sur les barrettes A et B, fiche à gauche sur la barrette C). Sur la colonne 2, nous avons mis 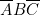 . Sur la colonne 3, il y a
. Sur la colonne 3, il y a 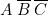 Sur la colonne 4, il y a
Sur la colonne 4, il y a 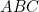
- — Pour « alimenter » la lampe
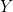 , il suffit d’une seule « colonne de programmation ». Nous avons choisi la colonne 5. Pour « écrire »
, il suffit d’une seule « colonne de programmation ». Nous avons choisi la colonne 5. Pour « écrire » 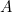 , il suffit de placer une fiche à gauche de la colonne 5, sur la barrette
, il suffit de placer une fiche à gauche de la colonne 5, sur la barrette 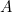 et de « neutraliser»
et de « neutraliser» 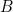 et
et 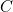 en plaçant deux fiches de part et d’autre de la colonne 5 sur les barrettes
en plaçant deux fiches de part et d’autre de la colonne 5 sur les barrettes 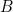 et
et 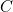 .
. - — Pour la lampe Z, il faut deux colonnes. Nous avons choisi les colonnes de programmation 6 et 7. Sur la colonne 6, nous avons placé
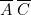 ; sur la colonne 7,
; sur la colonne 7, 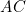
- — Ainsi est justifié le programme présenté sur la notice
 .
.
Jouez

- — Pour « alimenter » la lampe
- — Si, par exemple, la 2