Notice 9 et 10Jeu de cartes et stratégie |
- 1° Analyse du problème
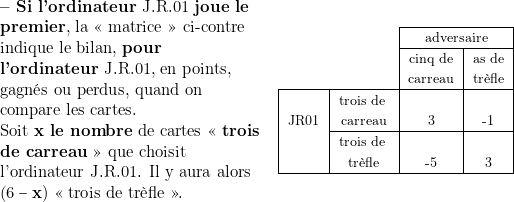
Le bilan pour l’ordinateur J.R.01 est alors :
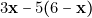 dans le cas où l’adversaire choisit le « cinq de carreau » et
dans le cas où l’adversaire choisit le « cinq de carreau » et 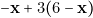 s’il choisit « l’as de trèfle
». Le gain sera le même, pour J.R.01, si
s’il choisit « l’as de trèfle
». Le gain sera le même, pour J.R.01, si ![Rendered by QuickLaTeX.com \[ 3\mathbf{x}-5(6-\mathbf{x})=\mathbf{-x}+3(6-\mathbf{x}) \]](https://jr01.dhenin.fr/wp-content/ql-cache/quicklatex.com-9fb46f81daa4c7a68d4953930f0fa9d5_l3.png)
On obtient
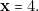 L’ordinateur J.R.01 doit donc choisir 4 cartes « trois de carreau » et 2 cartes « trois de trèfle ». Son gain sera alors toujours de
L’ordinateur J.R.01 doit donc choisir 4 cartes « trois de carreau » et 2 cartes « trois de trèfle ». Son gain sera alors toujours de ![Rendered by QuickLaTeX.com \[ 3\times2-5(6-2)=2 \; \mathrm{points} \]](https://jr01.dhenin.fr/wp-content/ql-cache/quicklatex.com-99d03e8f139d7e11be04f80bcc63fc03_l3.png)
- Si l’adversaire de J.R. 01 joue le premier.
- S’il ne place pas de trèfles, il est clair que le J.R. 01 doit choisir « trèfle ».
- S’il place un seul trèfle, le J.R.01 a encore avantage à choisir « trèfle ».
- S’il place deux cartes « trèfle » ou plus, le calcul montre que le J.R. 01 doit choisir un « carreau ».
Le problème est donc résolu.
Mais… l’ordinateur J.R. 01 peut faire beaucoup mieux c’est-à-dire offrir plus de stratégies différentes (notice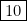 ). Aussi a-t-on cherché à ne faire qu’un seul programme pour les quatre jeux présentés sur les notices
). Aussi a-t-on cherché à ne faire qu’un seul programme pour les quatre jeux présentés sur les notices  et
et 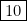 . L’étude de tous les cas vous conduira à la table de valeurs ci-dessous.
. L’étude de tous les cas vous conduira à la table de valeurs ci-dessous. - 2° Table de valeurs.
![Rendered by QuickLaTeX.com \begin{tabular}{rrr|r|c|c||c|c|c|c} \multicolumn{1}{c}{\textsf{\large{}$ $}} & \multicolumn{1}{c}{\textsf{\large{}$ $}} & \multicolumn{1}{c}{\textsf{\large{}$ $}} & \multicolumn{3}{c}{\textsf{\large{}$\begin{array}{c} {\scriptscriptstyle entr\acute{e}e}\\ \overbrace{\qquad\qquad} \end{array}$}} & \multicolumn{3}{c}{\textsf{\large{}$\begin{array}{c} {\scriptscriptstyle sortie}\\ \overbrace{\qquad\qquad} \end{array}$}} & \\ \cline{4-9} & & \multirow{5}{2cm}{{\tiny{}nombre de cartes de trèfles placées {[}0, 1, 2 (3 ou plus)}} & \textsf{\Large{}A} & \textsf{\Large{}B} & \textsf{\Large{}C} & \textsf{\Large{}X} & \textsf{\Large{}Y} & \textsf{\Large{}Z} & \\ \cline{4-9} \multicolumn{1}{c}{\multirow{4}{1.2cm}{{\tiny{}}% \begin{minipage}[t]{1.2cm}% \begin{singlespace} \noindent {\tiny{}l'adversaire joue le 1er}\end{singlespace} \end{minipage}}} & \multicolumn{1}{c}{\multirow{4}{1mm}{ $\left\updownarrow\vbox to 9mm{}\right.$} } & \multicolumn{1}{c|}{} & \multicolumn{1}{c|}{{\large{}0}} & {\large{}0} & {\large{}0} & {\large{}0} & {\large{}0} & {\large{}0} & \multirow{4}{2.1cm}{{\tiny{}carte à choisir par JR01 « carreau » : 1 « trèfle » : 0}}\\ \cline{4-9} \multicolumn{1}{c}{} & \multicolumn{1}{c}{} & \multicolumn{1}{c|}{} & \multicolumn{1}{c|}{{\large{}0}} & {\large{}0} & {\large{}1} & {\large{}0} & {\large{}0} & {\large{}0} & \\ \cline{4-9} \multicolumn{1}{c}{} & \multicolumn{1}{c}{} & \multicolumn{1}{c|}{} & \multicolumn{1}{c|}{{\large{}0}} & {\large{}1} & {\large{}0} & {\large{}0} & {\large{}0} & {\large{}1} & \\ \cline{4-9} \multicolumn{1}{c}{} & \multicolumn{1}{c}{} & \multicolumn{1}{r|}{} & \multicolumn{1}{c|}{{\large{}0}} & {\large{}1} & {\large{}1} & {\large{}0} & {\large{}0} & {\large{}1} & \\ \hline \hline \multicolumn{1}{c}{\multirow{4}{1.2cm}{{\tiny{}JR01 joue le 1er}}} & \multicolumn{1}{c}{\multirow{4}{1mm}{$\left\updownarrow\vbox to 7mm{}\right.$}} & \multicolumn{1}{c|}{\multirow{4}{2cm}{{\tiny{}nombre total de cartes à placer (option 1 2 ou 3)}}} & \multicolumn{1}{c|}{{\large{}1}} & {\large{}1} & {\large{}0} & {\large{}1} & {\large{}0} & {\large{}0} & \multirow{3}{2.1cm}{{\tiny{}nombre de cartes de carreaux que doit jouer JR01}}\\ \cline{4-9} \multicolumn{1}{c}{} & \multicolumn{1}{c}{} & \multicolumn{1}{c|}{} & \multicolumn{1}{c|}{{\large{}1}} & {\large{}0} & {\large{}1} & {\large{}1} & {\large{}0} & {\large{}0} & \\ \cline{4-9} \multicolumn{1}{c}{} & \multicolumn{1}{c}{} & \multicolumn{1}{c|}{} & \multicolumn{1}{c|}{{\large{}1}} & {\large{}0} & {\large{}0} & {\large{}0} & {\large{}1} & {\large{}1} & \\ \cline{4-9} \end{tabular}](https://jr01.dhenin.fr/wp-content/ql-cache/quicklatex.com-6cdccabb395009ace81faa2c5bd93f51_l3.png)
- 3° Expressions algébriques.
D’après la table ci-dessus vous montrerez aisément que
![Rendered by QuickLaTeX.com \[ X=\left|\begin{array}{c} AB\overline{C}\\ A\overline{B}C \end{array}\right| \qquad Y=A\;\overline{B}\;\overline{C}; \qquad Z=\left|\begin{array}{c} \overline{A}B\overline{C}\\ \;\overline{A}BC\\ A\;\overline{B}\;\overline{C} \end{array}\right| \]](https://jr01.dhenin.fr/wp-content/ql-cache/quicklatex.com-cf2b84b8dd2d878b4170f651ebb40dc4_l3.png)
- 4° Simplification.
Seule l’expression de
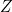 se simplifie. On obtient
se simplifie. On obtient 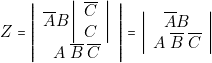
- 5° Schéma de programme.
Cherchez à dessiner ce programme. Vous devez obtenir celui décrit dans la notice

Jouez 
|
