Notice 7Une belle réussite ou un échec partiel ? |
-
1° Analyse du problème.
- — deux rois,
- – un roi (1
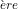 carte regardée, voir notice
carte regardée, voir notice  ) et un valet deuxième carte regardée).
) et un valet deuxième carte regardée).
- – une dame (1
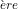 carte regardée) et un roi (deuxième carte regardée).
carte regardée) et un roi (deuxième carte regardée).
- 2° Table de valeurs.
Les réponses aux 3 questions posées (voir notice
 pouvant pas être 3 fois oui, la table n’a que 7 lignes par suppression de la ligne
pouvant pas être 3 fois oui, la table n’a que 7 lignes par suppression de la ligne 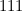 . Rappelons que l’on code à l’entrée :
. Rappelons que l’on code à l’entrée : 
Et qu’à la sortie, nous codons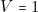 pour la réussite totale ;
pour la réussite totale ; 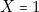 pour la réussite du paquet des valets ;
pour la réussite du paquet des valets ; 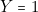 pour celle du paquet des dames ;
pour celle du paquet des dames ; 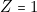 , dans les cas où il peut y avoir en plus de la réussite des rois une autre réussite, sans qu’elle soit totale.
, dans les cas où il peut y avoir en plus de la réussite des rois une autre réussite, sans qu’elle soit totale.
D’où la table ci-après :
- 2° Expressions algébriques.
- — La lampe
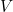 , s’allume sur la deuxième ligne seule. Donc
, s’allume sur la deuxième ligne seule. Donc 
- — La lampe
 doit s’allumer sur les lignes 2 ou 4. Or la ligne 2 correspond à (
doit s’allumer sur les lignes 2 ou 4. Or la ligne 2 correspond à (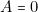 et
et 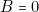 et
et 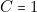 ) soit pour
) soit pour 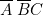 . La ligne 4 correspond à (
. La ligne 4 correspond à (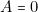 et
et 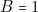 et
et 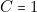 ) soit à
) soit à 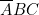 . Donc :
. Donc : 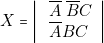
- — La lampe
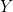 doit s’allumer sur les lignes 2 ou 6. Or la ligne 2 correspond à (
doit s’allumer sur les lignes 2 ou 6. Or la ligne 2 correspond à (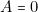 et \textbf{
et \textbf{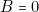 } et
} et 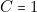 ) soit à
) soit à 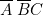 . La ligne 6 correspond à (
. La ligne 6 correspond à (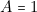 et
et 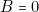 et
et 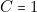 ) soit
) soit 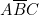 . Donc :
. Donc : 
- — La lampe
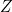 est allumée sur les lignes 1, 3, 5. Par suite
est allumée sur les lignes 1, 3, 5. Par suite 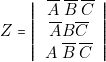
- — La lampe
-
4° Simplifications (voir 1
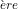 partie, paragraphes 6 et 8). }
partie, paragraphes 6 et 8). }
![Rendered by QuickLaTeX.com \[X=\left|\begin{array}{c} \overline{A}\;\overline{B}C\\ \overline{A}BC \end{array}\right|= \overline{A}C ; \qquad Y=\left|\begin{array}{c} \overline{A}\\ A \end{array}\right|\overline{B}C=\;\overline{B}C\qquad Z=\left|\begin{array}{c} \;\overline{A}\;\overline{B}\;\overline{C}\\ \overline{A}B\overline{C}\\ A\;\overline{B}\;\overline{C} \end{array}\right|=\left|\begin{array}{c} \;\overline{A}\;\overline{C}\\ A\;\overline{B}\;\overline{C} \end{array}\right|\]](https://jr01.dhenin.fr/wp-content/ql-cache/quicklatex.com-762260c857d2c6239fe27d9b1463e447_l3.png)
- 4° Schéma du programmevoir notice
 )
)
- — Pour
 , un seul branchement suffit. Nous avons choisi la colonne de programmation 2 . On a neutralisé
, un seul branchement suffit. Nous avons choisi la colonne de programmation 2 . On a neutralisé 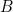 avec les deux fiches indiquée sur la barrette
avec les deux fiches indiquée sur la barrette 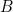 et les deux autres réalisent
et les deux autres réalisent  ;
;
- — Pour
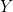 , un seul branchement suffit. Nous avons choisi la colonne 4 et réalisé
, un seul branchement suffit. Nous avons choisi la colonne 4 et réalisé  ;
;
- — Pour
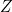 , deux branchements sont nécessaires. On a choisi les colonnes 6 et 7.
, deux branchements sont nécessaires. On a choisi les colonnes 6 et 7.
- — Pour marquer l’événement d’une réussite totale, nous avons utilisé la lampe
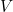 . Or
. Or  . Nous avons réalisé cela avec la « colonne de programmation » marquée 1 et reliée à la lampe
. Nous avons réalisé cela avec la « colonne de programmation » marquée 1 et reliée à la lampe 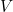 .
.
- — Ceci justifie le schéma de programme proposé notice
 .
.
- — Pour
Puisque l’on commence par retourner la carte située sur le paquet des rois, on s’aperçoit rapidement que, dans tous les cas, le paquet des rois donnera toujours une réussite (les quatre rois faces visibles).
Si donc la dernière carte du paquet placé en ![]() (ou de celui placé en
(ou de celui placé en ![]() ) est un roi, cette carte sera utilisée et, par suite, le paquet de valets (ou celui des dames) donnera une réussite (les quatre valets
faces visibles). Or si le paquet des valets est bien en place et si la dernière carte du paquet placé en
) est un roi, cette carte sera utilisée et, par suite, le paquet de valets (ou celui des dames) donnera une réussite (les quatre valets
faces visibles). Or si le paquet des valets est bien en place et si la dernière carte du paquet placé en ![]() est un valet, cette carte sera utilisée et, par suite, le paquet des dames donnera aussi une réussite. Celle-ci sera donc totale.
est un valet, cette carte sera utilisée et, par suite, le paquet des dames donnera aussi une réussite. Celle-ci sera donc totale.
Les cas certains de réussite totale sont donc, pour les deux cartes regardées :
Jouez 
|
