Notice 5Un jeu de dé |
- 1° Analyse du problème.
On connaît le total des trois nombres sans aucun renseignement sur les deux derniers, parce que la somme de ces deux derniers est toujours 7. En effet, sur un dé, la somme des nombres portés sur deux faces opposées est 7 (1 + 6 ou 2 + 5 ou 3 + 4).
Par suite, pour obtenir la table de valeur, il suffit de reprendre celle de la notice (§ 4) et d’ajouter 7 aux nombres écrits à la sortie, en remarquant que :
(§ 4) et d’ajouter 7 aux nombres écrits à la sortie, en remarquant que : - — le cas
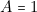 ,
, 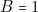 ,
, 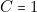 qui correspond à l’apparition (ou au choix dans le cas de la notice
qui correspond à l’apparition (ou au choix dans le cas de la notice  du nombre 0 ne peut se produire ;
du nombre 0 ne peut se produire ;
- — d’autre part, le cas
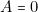 ,
, 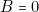 ,
, 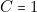 qui correspond, à la sortie (voir § 4), au nombre 7, ne peut pas se produire non plus. (Sur un dé les faces sont numérotées de 1 à 6) .
qui correspond, à la sortie (voir § 4), au nombre 7, ne peut pas se produire non plus. (Sur un dé les faces sont numérotées de 1 à 6) .
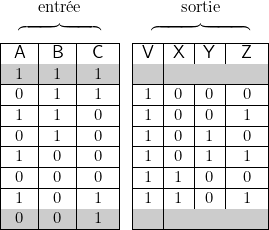
La table de valeur n’a que six lignes (1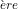 et 8
et 8 lignes exclues).
lignes exclues). - — le cas
- 2° Table de valeurs.
On prend donc celle du § 4 et on ajoute, à la sortie, 7 (c’est-à-dire 111 en binaire) sur chaque ligne (voir 1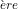 partie,§ 10).
partie,§ 10). Ainsi :
- 1
 ligne :
ligne : 
- 2
 ligne :
ligne : 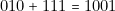
- 3
 ligne :
ligne : 
- 4
 ligne :
ligne : 
-
 ligne :
ligne : 
- 6
 ligne :
ligne : 
Ces résultats montrent qu’à la sortie il est nécessaire d’utiliserquatre lampes. On utilisera donc la lampe ![]() .
.
-
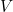 prend toujours la valeur 1.
prend toujours la valeur 1.
-
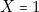 sur les lignes 5 ou 6, c’est-à-dire si (
sur les lignes 5 ou 6, c’est-à-dire si (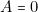 et
et 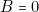 et
et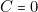 ) ou (
) ou (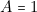 et
et 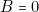 et
et 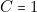 ).
).
Ceci correspond à :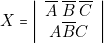
-
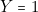 sur les lignes 3 ou 4, ce qui correspond à :
sur les lignes 3 ou 4, ce qui correspond à :
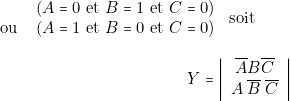
-
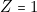 sur les lignes 2 ou 4 ou 6. C’est-à-dire :
sur les lignes 2 ou 4 ou 6. C’est-à-dire :
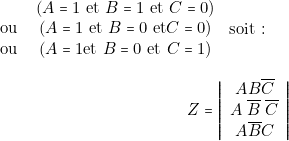
Seule l’expression de ![]() se simplifie. On obtient :
se simplifie. On obtient :
![Rendered by QuickLaTeX.com \[ Z=A\left|\begin{array}{c} B\overline{C}\\ \overline{B}\;\overline{C}\\ \overline{B}C \end{array}\right|=A\left|\begin{array}{c} \overline{B}\\ \overline{C} \end{array}\right|=\left|\begin{array}{c} A\overline{B}\\ A\overline{C} \end{array}\right| \]](https://jr01.dhenin.fr/wp-content/ql-cache/quicklatex.com-571f50a4a7f400ddbee1ed2cc0be9a21_l3.png)
- La lampe
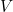 doit être toujours allumée. Nous l’avons donc reliée à une colonne de programmation (la colonne 1) en plaçant des fiches qui « neutralisent »
doit être toujours allumée. Nous l’avons donc reliée à une colonne de programmation (la colonne 1) en plaçant des fiches qui « neutralisent » 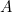 ,
, 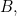
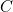 . D’où
. D’où 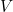 toujours allumée.
toujours allumée.
- La lampe
 doit être reliée à \textbf{deux} colonnes de programmation. Nous avons choisi les colonnes 2 et 3. Sur 2, nous avons représenté
doit être reliée à \textbf{deux} colonnes de programmation. Nous avons choisi les colonnes 2 et 3. Sur 2, nous avons représenté 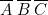 ; sur 3,
; sur 3, 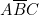 . D’où
. D’où 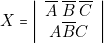
- La lampe
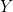 doit être reliée à \textbf{deux} colonnes de programmation. Nous avons choisi les colonnes 4 et 5. Sur 4, nous avons réalisé
doit être reliée à \textbf{deux} colonnes de programmation. Nous avons choisi les colonnes 4 et 5. Sur 4, nous avons réalisé 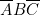 et sur la 5,
et sur la 5, 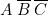 . D’où
. D’où 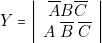
- De même la lampe
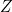 doit être reliée à deux colonnes de programmation. Sur la colonne 6, nous avons réalisé
doit être reliée à deux colonnes de programmation. Sur la colonne 6, nous avons réalisé 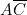 (B est « neutralisée ») ; sur 7, nous obtenons
(B est « neutralisée ») ; sur 7, nous obtenons 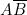 (C est « neutralisée »).
Donc
(C est « neutralisée »).
Donc 
- Ceci justifie le schéma de programme présenté sur la notice
 .
.
Jouez 
|
