Les seize opérateurs binaires |
Au lieu de partir de l’usage et de s’interroger sur la façon de représenter au mieux un opérateur comme et, ou, etc, il est possible de procéder de façon formelle. Un opérateur binaire quelconque, disons ![]() est tel que, appliqué à deux propositions
est tel que, appliqué à deux propositions ![]() et
et ![]() , il
engendre une proposition
, il
engendre une proposition ![]() . Si l’on adopte l’ordre canonique pour les valeurs de
. Si l’on adopte l’ordre canonique pour les valeurs de ![]() et de
et de![]() , l’évaluation de
, l’évaluation de ![]() est
fournie par un quadruple (a b c d) où a, b, c et
est
fournie par un quadruple (a b c d) où a, b, c et ![]() ont soit la valeur 1 soit la valeur 0 et ce quadruple détermine entièrement l’opérateur
ont soit la valeur 1 soit la valeur 0 et ce quadruple détermine entièrement l’opérateur ![]() .
.
Laissons pour l’instant la question de l’interprétation possible des opérateurs et cherchons simplement à les dénombrer exhaustivement.
On aura cinq cas à étudier.
I. (a b c d) ne contient que des 0 ;
1 façon : (0000)
II. (a b c d) contient un 1 et trois 0 ;
4 façons : (1 0 0 0) (0 1 0 0) (0 0 1 0) (0 0 0 1)
III. (a b c d) contient deux 1 et deux 0 ;
6 façons : (1 1 0 0) (1 0 1 0) (0 1 1 0) (1 0 0 1) (0 1 0 1) (0 0 1 1)
IV. (a b c d) contient trois 1 et un 0 ;
4 façons : (1 1 1 0) (1 1 0 1) (1 0 1 1) (0 1 1 1)
V. (a b c d) ne contient que des 1.
1 façon : (1111).
Il existe donc 16 et seulement 16 opérateurs binaires possibles.
Remarque
On aurait pu trouver ce résultat d’une autre façon encore. Un opérateur binaire peut se concevoir comme une application dont l’ensemble de départ est l’ensemble des couples (ordonnés) :
![]() et dont l’ensemble d’arrivée est l’ensemble
et dont l’ensemble d’arrivée est l’ensemble ![]() . Si
. Si ![]() , un opérateur binaire est donc une application
, un opérateur binaire est donc une application ![]() où
où ![]() représente l’ensemble produit
représente l’ensemble produit ![]() par
par ![]() . Il suffit de dénombrer les applications
. Il suffit de dénombrer les applications ![]() ce que fait le tableau suivant, pour retrouver (cette fois-ci en colonne) les 16 quadruples.
ce que fait le tableau suivant, pour retrouver (cette fois-ci en colonne) les 16 quadruples.

Il est possible de tirer davantage encore de ce qui précède. Soit ![]() une proposition quelconque qui contient les deux atomes
une proposition quelconque qui contient les deux atomes ![]() et
et ![]() . Ceux-ci peuvent figurer un nombre quelconque de fois dans
. Ceux-ci peuvent figurer un nombre quelconque de fois dans ![]() et les compositions peuvent se faire à l’aide d’un ou de plusieurs des seize opérateurs.
et les compositions peuvent se faire à l’aide d’un ou de plusieurs des seize opérateurs.
Exemple
![]() =df
=df ![]()
Dans tous les cas, l’évaluation de ![]() conduira à l’un des seize quadruples ci-dessus. Ce sera (1 1 1 0) pour cet exemple (V, p. 8), qui est aussi l’évaluation de
conduira à l’un des seize quadruples ci-dessus. Ce sera (1 1 1 0) pour cet exemple (V, p. 8), qui est aussi l’évaluation de ![]() .
.
Cela signifie que ![]() est équivalente à
est équivalente à ![]() , donc que
, donc que
![]() ou encore
ou encore
![]()
L’ensemble ![]() de toutes les propositions qui contiennent deux atomes est infini, puisque chaque atome peut être répété un nombre quelconque de fois et la relation d’équivalence
de toutes les propositions qui contiennent deux atomes est infini, puisque chaque atome peut être répété un nombre quelconque de fois et la relation d’équivalence ![]() engendre une partition de
engendre une partition de ![]() en 16 classes d’équivalence. Nous noterons
en 16 classes d’équivalence. Nous noterons ![]() la classe de toutes les propositions dont l’évaluation est
la classe de toutes les propositions dont l’évaluation est ![]() .
.
Exemples
1) Comme nous venons de le voir ![]() ,
, ![]() ;
;
2) on s’assurera que ![]() ,
, ![]() , et que
, et que ![]() .
.
Il est aussi possible de désigner la classe ![]() en choisissant l’un quelconque de ses éléments et en le plaçant entre crochets. Ainsi, par exemple,
en choisissant l’un quelconque de ses éléments et en le plaçant entre crochets. Ainsi, par exemple, ![]() désignera la classe
désignera la classe ![]() , {[}
, {[}![]() {]} désignera
{]} désignera ![]() , etc.
, etc.
Ordonnons maintenant les 16 classes. Nous dirons que la classe ![]() précède la classe
précède la classe ![]() , et nous noterons
, et nous noterons ![]() , si un représentant quelconque de
, si un représentant quelconque de ![]() implique, au sens de la relation
implique, au sens de la relation ![]() , un représentant quelconque de la classe
, un représentant quelconque de la classe ![]() .
.
Exemple
Soit les trois classes ![]() ,
, ![]() et
et ![]() . On s’assure sans peine que :
. On s’assure sans peine que : ![]() ,
, ![]() et
et ![]() .
.
D’autre part, le calcul montre que :
![]() ,
,
![]() ,
,
![]() .
.
On aura donc les implications :
![]() ,
, ![]() ,
,
![]() .
.
Et il s’ensuit que :
![]() ,
, ![]() et
et ![]() . La troisième relation découle des deux premières par la transitivité de la relation « précède », qui est une relation d’ordre.
. La troisième relation découle des deux premières par la transitivité de la relation « précède », qui est une relation d’ordre.
Remarques
1) ![]() . En effet, cela revient à dire que
. En effet, cela revient à dire que ![]() est une tautologie, ce que montre le calcul suivant :
est une tautologie, ce que montre le calcul suivant :

Il aurait donc été possible de choisir ![]() comme représentant de la classe
comme représentant de la classe ![]() . Cela exige toutefois de se souvenir que
. Cela exige toutefois de se souvenir que ![]() n’est pas ici une proposition isolée, mais bien la seconde de deux atomes. Pour garder la chose en mémoire, nous écrirons
n’est pas ici une proposition isolée, mais bien la seconde de deux atomes. Pour garder la chose en mémoire, nous écrirons ![]() pour représenter la classe qui contient, en particulier la proposition
pour représenter la classe qui contient, en particulier la proposition ![]() , mais qui contient aussi des propositions où l’atome
, mais qui contient aussi des propositions où l’atome![]() figure explicitement.
figure explicitement.
2) D’une façon toute semblable, nous écrirons ![]() pour la classe
pour la classe ![]() ,
, ![]() pour la classe
pour la classe ![]() et
et ![]() pour la classe~
pour la classe~![]() .
.
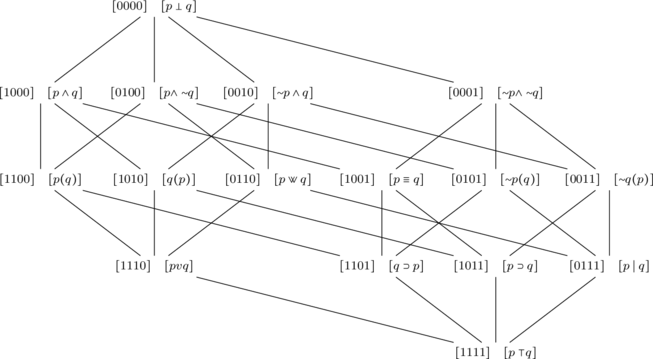
Cela dit, il est possible d’ordonner les 16 classes d’équivalence comme le montre le diagramme précédent. On s’assurera par le calcul que les propositions choisies appartiennent bien aux classes correspondantes. Enfin nous avons écrit ![]() pour désigner l’opérateur tel que
pour désigner l’opérateur tel que ![]() et
et ![]() pour représenter celui tel que
pour représenter celui tel que ![]() .
.
Ce schéma a cinq niveaux et il est disposé de telle façon que si une classe de niveau ![]() est reliée à une classe de niveau
est reliée à une classe de niveau ![]() , elle la précède. Ainsi
, elle la précède. Ainsi ![]() . Toutefois deux classes quelconques ne sont pas toujours reliées : on a affaire à un ordre partiel. Les
. Toutefois deux classes quelconques ne sont pas toujours reliées : on a affaire à un ordre partiel. Les
classes d’un même niveau ne sont pas ordonnées entre elles, et il n’est pas non plus possible de comparer ![]() par exemple à
par exemple à ![]() .
.
Si l’on revient à la définition que nous avons donnée de la relation ![]() , le même schéma permet de lire les implications entre les propositions, donc les tautologies.
, le même schéma permet de lire les implications entre les propositions, donc les tautologies.
Exemples
![]() ;
; ![]() ;
; ![]() .
.
Enfin la proposition notée ![]() implique toutes les autres. Elle correspond à la contradiction et ce fait traduit partiellement l’adage ex falso quodlibet sequitur. Réciproquement, toute proposition implique celle notée
implique toutes les autres. Elle correspond à la contradiction et ce fait traduit partiellement l’adage ex falso quodlibet sequitur. Réciproquement, toute proposition implique celle notée ![]() . La chose se comprend facilement puisque
. La chose se comprend facilement puisque ![]() correspond à la notion de tautologie. Soit
correspond à la notion de tautologie. Soit ![]() une proposition dont l’évaluation est (\emph{a b c d}). Formons la conditionnelle
une proposition dont l’évaluation est (\emph{a b c d}). Formons la conditionnelle ![]() . On aura :
. On aura :
![Rendered by QuickLaTeX.com \begin{tabular}{l>{\raggedleft}m{0.15\textwidth}} \begin{tabular}{>{\raggedleft}m{0.15\textwidth}|cccc} P & \emph{a} & \emph{b} & \emph{c} & \emph{d}\tabularnewline $p\top q$ & 1 & 1 & 1 & 1\tabularnewline \hline \hline $P\supset(p\top q)$ & 1 & 1 & 1 & 1\tabularnewline \end{tabular} & % \parbox[t]{0.65\columnwidth}{% En effet, si $a$ est 1, on a bien $val(1\supset1)=1$ \\ et si $a$ est 0 on a aussi $val(0\supset1)=1.$\\ De même avec b, c et d.% }\tabularnewline \end{tabular}](https://jr01.dhenin.fr/wp-content/ql-cache/quicklatex.com-4b133125061d957f30160bfcd5fb3743_l3.png)
Remarques
1) Soit ![]()
![]() et
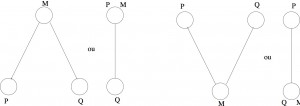
et![]() trois propositions qui ont entre elles les relations de la figure 2. Alors
trois propositions qui ont entre elles les relations de la figure 2. Alors ![]() est
est ![]() . De même si
. De même si ![]() ,
, ![]() et
et ![]() ont entre elles les relations de la figure 3,
ont entre elles les relations de la figure 3, ![]() est
est ![]() .\smallskip{}
.\smallskip{}
![]() ;
; ![]() \\
\\
![]() ;
; ![]()
2) La structure représentée à la figure 1 est isomorphe à celle de l’ensemble des parties d’un ensemble ![]() à 4 éléments. Elle constitue de plus un exemple d’algèbre de Boole (V. Fascicule III).
à 4 éléments. Elle constitue de plus un exemple d’algèbre de Boole (V. Fascicule III).