La proposition conjonctive |
Une proposition conjonctive est de la forme : 
et 
. Nous écrirons 
, ce que certains auteurs notent~ : 
, 
ou même simplement 
.
Supposons qu’une telle proposition, par exemple « il fait grand froid et j’ai tué six loups » soit vraie. L’usage habituel de la conjonction « et » est tel que nous entendons que « il fait grand froid » et « j’ai tué six loups » sont également deux propositions vraies. Ceci conduit à poser les deux règles d’élimination suivantes, que nous désignerons par le même sigle : 
e.
Règles 
e
Inversement d’ailleurs, dans le cas où l’on sait que les deux propositions et sont vraies séparément, nous sommes disposés à affirmer que la proposition conjonctive est aussi vraie. D’où la règle i :
Règle i
Remarque
| Ici encore les petites barres en traitillé indiquent que les propositions qui sont au-dessus sont les prémisses de la règle et que la proposition qui est au-dessous en est la conclusion. |
L’emploi de ces règles est extrêmement facile. En voici quelques exemples.
Exemples
[1] 
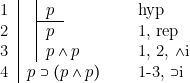
[2] 
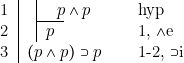
[3] 
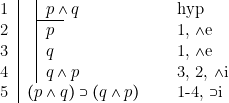
Remarque : Aucune hypothèse n’a été faite, dans l’énoncé des règles, sur la relation entre 
et 
. Il s’ensuit qu’elles sont applicables aussi bien lorsque 
que lorsque 
.
[4]
Remarque : au lieu de répéter la donnée à la dernière ligne d’une démonstration, nous écrirons souvent « Th. », abréviation pour « le théorème à démontrer ».
[5]
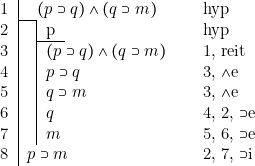
Comme on le voit sur cet exemple, la procédure heuristique décrite à la fin du paragraphe ? ?, reste applicable ici. Après avoir pris comme hypothèses tous les antécédents possibles, on décompose entièrement les propositions pour « reconstruire » ensuite le tout.