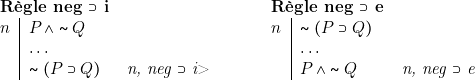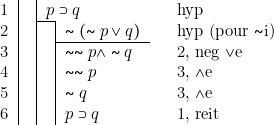JR01

Proposition disjonctive

La négation

Quelques propriétés de la logique des propositions

Jusqu’ici, nous avons admis que, dans les applications, nous traiterions comme atomiques aussi bien les propositions affirmatives que les propositions négatives. Il est toutefois clair que toute proposition négative, disons , peut se comprendre comme la négation d’une proposition affirmative : non–.

Exemples

[1] « 6 n’est pas un nombre premier », soit peut se comprendre comme :
« non : 6 est un nombre premier », soit non-–.

[2] « Il n’y a pas de roses sans épines » peut se comprendre comme :
« non : il y a des roses sans épines ».

Le mot « non » joue encore le rôle d’un foncteur propositionnel, mais c’est un foncteur unaire, en ce sens qu’il s’applique à une seule proposition. Il désigne l’opération qui transforme une proposition en sa négation non. Nous noterons , ce que d’autres écrivent aussi ou ou .

Il est facile de voir que la négation joue un rôle privilégié en logique. On peut tout d’abord s’assurer sur soi-même qu’il n’est pas immédiat que la négation de « il est bête et méchant » soit « il n’est pas bête ou il n’est pas méchant ». On peut aussi constater que des logiques, comme la logique intuitionniste ou la logique minimale, diffèrent avant tout de la logique classique par l’usage qu’elles font de la négation. Ceci suffit déjà à expliquer pourquoi nous allons procéder en plusieurs étapes et examiner chaque fois la portée des règles introduites.

Règle i

Commençons par poser que, si une proposition , prise comme hypothèse, conduit à une contradiction — c’est-à-dire qu’il est possible d’en déduire une proposition et la négation de — alors c’est qu’il faut affirmer. Cela nous donne :

Règle i

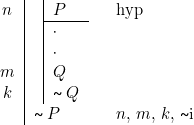
Remarques

1) Il s’agit ici d’une règle qui codifie, dans notre système, le raisonnement par l’absurde : toute proposition qui conduit à une contradiction doit être niée. 2) Cette règle est très proche de la règle i, en ce sens qu’elle permet de se libérer d’une hypothèse. Toutefois la référence se fait aux seules propositions , et et non à toute la sous-déduction. 3) Cette règle se propose d’introduire un signe « », de même que la règle i, par exemple, servait à introduire un signe « ». Il y a cependant ici un élément qui peut paraître paradoxal. Si l’on convient de considérer que toute la sous-déduction constitue la prémisse de la règle, on constate que la prémisse contient nécessairement une mention du signe « » que la règle a pour but d’introduire ! Il est clair que le « » qui précède la proposition de la ligne ne saurait, sans cercle vicieux, être introduit par la règle. Il faut donc en conclure qu’il ne peut y figurer que s’il est préalablement contenu dans l’hypothèse . En conséquence, notre système ne permet de traiter de la négation que dans la mesure où nous prenons nous-mêmes en considération (pour en examiner les conséquences) des propositions elles-mêmes négatives ;. Cette sorte de restriction est liée à l’adage que, en logique, le vrai ne peut conduire au faux.

Exemples

[1]

[2]

Remarques

1) Il faut se garder de conclure que, puisque l’hypothèse conduit à une contradiction, c’est qui est la proposition correcte. Nous n’avons, pour le moment, aucune règle qui nous permette d’éliminer une négation. 2) L’exemple [2] permet d’écrire le métathéorème : . On aura donc l’implication qui est une partie du principe classique de la double négation. 3) Rien n’empêche aussi de s’en tenir (avec à la place de ) aux cinq première lignes de l’exemple [2] et de conclure à la règle dérivée suivante que nous désignerons par neg i (introduction « négative » de ) :

Règle neg i

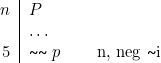
[3]

Remarques

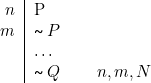
> Règle 2. On entend volontiers dire qu’« une contradiction conduit à n’importe quoi ». Ce que nous pouvons toutefois établir pour l’instant, c’est que : . En effet, cette implication signifie que , métathéorème qui découle immédiatement de la règle N. Nous pouvons donc, quant à nous, dire : « une contradiction conduit à la négation de n’importe quelle proposition ».

Dérivons maintenant directement trois nouvelles règles :
Règle neg i (pour introduire une conjonction précédée d’une négation)

Règle neg i (pour introduire une disjonction précédée d’une négation)

Règle neg e (pour éliminer une disjonction précédée d’une négation)

Faisons maintenant le point de la situation. Si nous ajoutons aux règles générales et aux règles pour les fondeurs , , et , la règle i, nous pouvons dériver les règles suivantes :

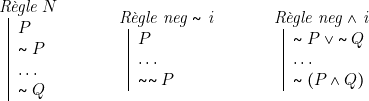
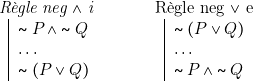
Les deux règles neg i et neg e constituent l’une des lois de Morgan. Il est tentant de se demander si l’on ne pourrait pas encore dériver la règle neg Ae (avec neg A j, nous obtiendrions l’autre loi de Morgan) et la règle neg e (avec neg i nous aurions la loi de double négation). En fait on peut montrer, par des considérations métathéoriques que nous ne rapporterons pas, que la chose n’est pas possible. Cela signifie que nous ne disposons, pour le moment, que d’une forme faible de la négation. On l’appelle parfois la réfutabilité et la logique obtenue équivaut à la logique dite minimale de Johansson (1936). (On trouvera des compléments d’information dans le Fascicule 3).

Comme la limitation fondamentale réside en ce que la règle N ne nous permet que d’arriver à une proposition négative , nous allons renforcer notre négation en introduisant l’équivalent du principe fameux : ex falso quodlibet sequitur. Nous poserons donc la nouvelle règle suivante :

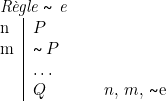
Remarques

1. Il est évidemment un peu abusif de considérer cette règle comme une règle d’élimination. La proposition de la conclusion peut fort bien désigner une proposition qui commence par une négation. Il est cependant commode d’adopter cette terminologie pour des raisons de symétrie. 2. Cette règle dispense de la règle en ce sens que toute déduction qui faisait usage de la règle peut être refaite en utilisant la règle e. 3. Cette nouvelle règle est cependant plus forte que la règle N, ce qui signifie qu’elle permet de démontrer de nouveaux théorèmes. Exemple 4. Il est toutefois remarquable que nous ne puissions encore ni déduire les règles neg e, neg e, ni la réciproque du théorème ci-dessus. Examinons, par exemple, ce que donnerait une tentative de démontrer : On voit que, si l’on pouvait passer de à , il serait possible d’éliminer grâce à la ligne 6. Cela conduirait à et, en présence de (ligne 5), nous aurions la contradiction souhaitée. En fait nous pourrions écrire alors et il faudrait, une nouvelle fois, éliminer une double négation. %

Il s’ensuit que nous disposons maintenant d’un nouveau type de négation, plus fort que la réfutabilité mais pas encore « complet » au sens classique. Cette négation se nomme volontiers l’absurdité et le système obtenu en ajoutant aux règles de la logique minimale la règle e équivaut à la logique intuitionniste de Heyting (1930).

Pour terminer, donnons-nous la règle neg e :

Règle neg e

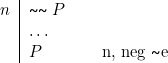
Nous venons d’esquisser la preuve qu’il est maintenant possible de démontrer ce qui permet d’affirmer que est équivalent à . Il est aussi facile de déduire la règle neg e qui manquait :

Règle neg e

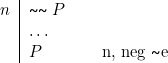
En effet :

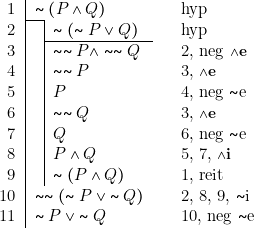
Le système engendré par les règles suivantes : règles générales, règles pour , , , règles i, e et neg e conduit à la {\it logique classique des propositions}. Le métathéorème suivant, dit \emph{principe du tiers exclu}, en est caractéristique :

Preuve

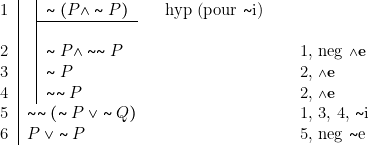
Remarques

1. Ainsi qu’on peut le constater, la ligne 5 s’obtient à l’aide de règles qui sont déjà disponibles en logique minimale. C’est donc bien l’élimination de la double négation qui est caractéristique de la logique classique. 2) Glivenko (1929), comparant la logique intuitionniste I et la logique classique C, a pu établir l’épithéorème suivant : Si alors et réciproquement. 3.En résumé, nous avons la suite de systèmes logiques suivante, suite dans laquelle tout théorème d’un système à gauche d’une flèche est aussi théorème des systèmes à droite, sans que la réciproque soit vraie : Règles générales + Règle i + Règle e + Règle neg e Règles i,

4. Le lecteur vérifiera qu’en logique classique il est possible de dériver les deux règles suivantes, qui sont très commodes à l’usage :

Proposition disjonctive

Quelques propriétés de la logique des propositions