Que peut-on découvrir avec trois informations ? |
|
 |
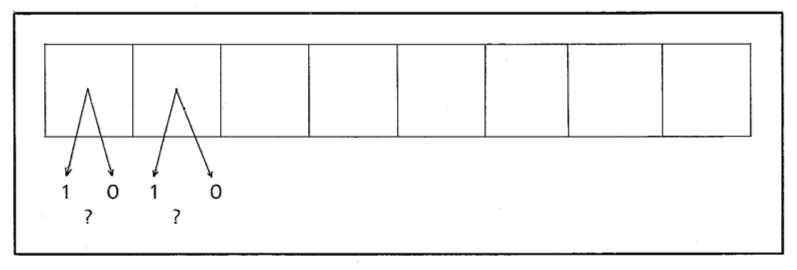
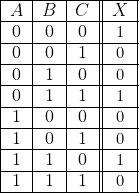
Autrement dit, nous avons 8 cases dans chacune desquelles il faut placer un 1 ou un 0. Deux choix à chaque case.
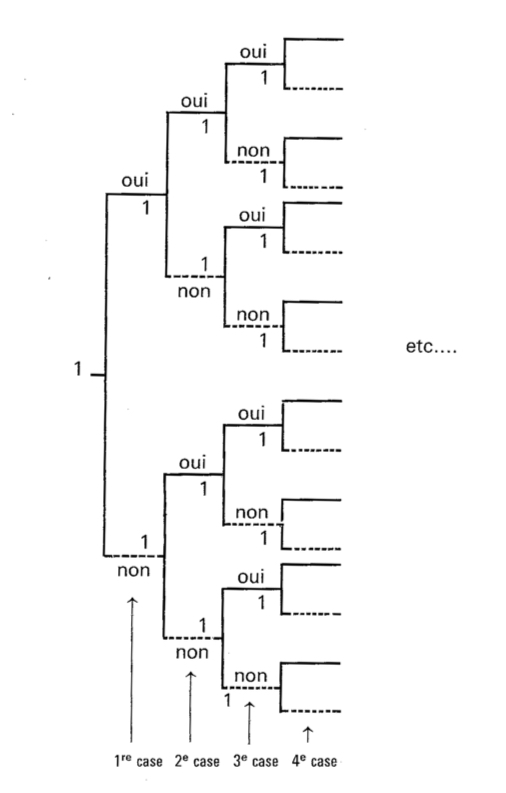
Comme il y a 8 cases, cela donne ![]() possibilités différentes. On peut schématiser cela de la façon suivante, en mettant oui si l’on prend 1, non si l’on prend 0.
possibilités différentes. On peut schématiser cela de la façon suivante, en mettant oui si l’on prend 1, non si l’on prend 0.
- Devons-nous construire 256 circuits logiques différents pour exprimer, à la sortie, ces 256 « programmes » ? Non, car on démontre que tout s’exprime à l’aide uniquement de et, ou ou non. Ainsi, par exemple, soit
 le « programme », la « proposition logique », définie par la table ci-dessous :
le « programme », la « proposition logique », définie par la table ci-dessous :
![Rendered by QuickLaTeX.com \begin{tabular}{|c|c|c||c|c|c|} \cline{1-4} \cline{6-6} {\large $A$} & {\large $B$} & {\large $C$} & {\large $X$} & & \\ \cline{1-4} \cline{6-6} {\large 0} & {\large 0} & {\large 0} & 1 & $\rightarrow$ & % \begin{minipage}[c]{1cm}% \smallskip{} $\overline{A}\;\overline{B}\;\overline{C}$\smallskip{} \end{minipage}\\ \cline{1-4} \cline{6-6} {\large 0} & {\large 0} & {\large 1} & 0 & & \\ \cline{1-4} \cline{6-6} {\large 0} & {\large 1} & {\large 0} & 0 & & \\ \cline{1-4} \cline{6-6} {\large 0} & {\large 1} & {\large 1} & 1 & $\rightarrow$ &% \begin{minipage}[c]{1cm}% \smallskip{} $\overline{A}BC$\smallskip{} % \end{minipage}\tabularnewline \cline{1-4} \cline{6-6} {\large 1} & {\large 0} & {\large 0} & 0 & & \\ \cline{1-4} \cline{6-6} {\large 1} & {\large 0} & {\large 1} & 0 & & \\ \cline{1-4} \cline{6-6} {\large 1} & {\large 1} & {\large 0} & 1 & $\rightarrow$ & % \begin{minipage}[c]{1cm}% \smallskip{} $AB\overline{C}$\smallskip{} % \end{minipage}\tabularnewline \cline{1-4} \cline{6-6} {\large 1} & {\large 1} & {\large 1} & 0 & & \\ \cline{1-4} \cline{6-6} \end{tabular}\label{Prog_X} % \end{center}](https://jr01.dhenin.fr/wp-content/ql-cache/quicklatex.com-72283555123db5eac1824eee252ec4f5_l3.png)
Comment exprimer
 ?
? D’après les règles de calculs des produits et des produels (voir §3 et §4 ), il est immédiat que :
![Rendered by QuickLaTeX.com \[ X=\left|\begin{array}{c} \bar{A}\bar{B}\bar{C}\\ \overline{A}BC\\ AB\overline{C}\end{array}\right|\]](https://jr01.dhenin.fr/wp-content/ql-cache/quicklatex.com-4253de9fb2fac8c7ec6f95b49d768151_l3.png)
Cet exemple montre comment on opérera dans tous les cas.
- Interprétation par montages électriques.
- Interprétations par l’ordinateur J.R. 01.
- — Celles-ci sont immédiates dès que l’on sait que :
- à gauche (en regardant le pupitre de l’ordinateur J.R. 01) de chaque colonne de programmation (notée de 1 à 7) une fiche enfoncée dans un trou correspond, suivant la barrette A, B, C considérée, soit à A, soit à B, soit à C.
- à droite de chaque colonne de programmation, une fiche enfoncée correspond soit à
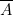 , soit à
, soit à 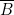 , soit à
, soit à 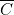 .
. - deux colonnes de programmation reliées à la même lampe de « sortie » correspond à « ou ».
- si l’on enfonce une fiche de part et d’autre d’une colonne de programmation on obtient soit
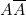 , soit
, soit 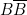 soit
soit 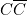 , qui est toujours vraie, donc on neutralise soit A, soit B, soit C.
, qui est toujours vraie, donc on neutralise soit A, soit B, soit C.
Ainsi pour programmer l’ordinateur J.R.~01 selon le programme
![Rendered by QuickLaTeX.com \[ X=\left|\begin{array}{c} \bar{A}\bar{B}\bar{C}\\ \overline{A}BC\\ AB\overline{C}\end{array}\right|\]](https://jr01.dhenin.fr/wp-content/ql-cache/quicklatex.com-9773f31b0bbcea67d99d6d66399f6748_l3.png)
- — on choisira trois colonnes de programmation, par exemple celles marquées 1, 2, 3 ;
- — on reliera ces colonnes à la lampe
 ;
; - — sur la colonne 1, on enfonce trois fiches : une à gauche sur A, une à gauche sur B, une à droite sur C (pour obtenir
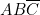 );
); - — sur la colonne 2, on enfonce trois fiches : une à droite sur A , une à gauche sur B, une à gauche sur C (pour obtenir
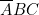 )
) - — sur la colonne 3, on enfonce trois fiches : une à droite sur A, à droite sur B, une à droite sur C (
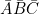 ).
).
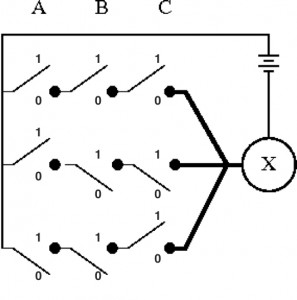
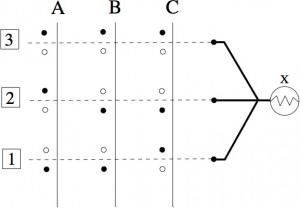
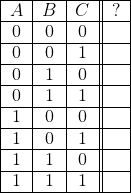
On obtient alors le programme ci-dessous (un rond plein indique une fiche enfoncée ; un rond « évidé » indique une absence de fiche).
- Vérifié-le ! Pour cela :
- — Celles-ci sont immédiates dès que l’on sait que :