Algèbre de Boole
|
- Deux relations courantes entre les 256 propositions que l’on peut former avec trois propositions, permettent de simplifier certaines expressions et, surtout, de simplifier les circuits électriques correspondants. Ces formules sont :
![Rendered by QuickLaTeX.com \[ \left|\begin{array}{c} AB\\ C\end{array}\right|=\left|\begin{array}{c} A\\ C\end{array}\right|\left|\begin{array}{c} B\\ C\end{array}\right| \]](https://jr01.dhenin.fr/wp-content/ql-cache/quicklatex.com-2b59b0b4827b933bd42d12919f9ed986_l3.png)
![Rendered by QuickLaTeX.com \[A\left|\begin{array}{c} B\\ C \\ \end{array}\right|=\left|\begin{array}{c} AB\\ AC\\ \end{array}\right| \]](https://jr01.dhenin.fr/wp-content/ql-cache/quicklatex.com-b3f4d33b3789c6154c5f3ddb6187b6ea_l3.png)
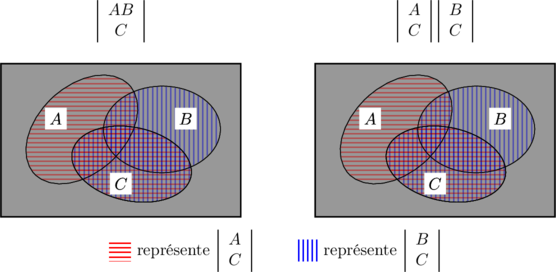
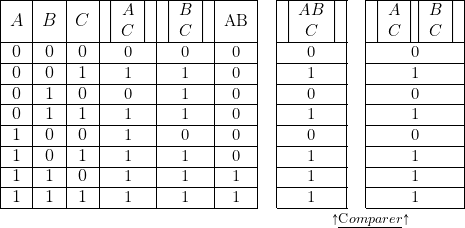
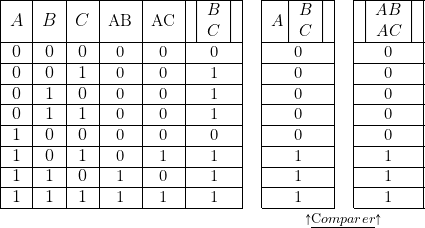
Les démonstrations des formules ci-dessus s’obtiennent soit à l’aide des diagrammes ensemblistes, soit, mieux, à l’aide des tables de valeur (voir ci-dessous).
- Démonstration de la première formule.
- Démonstration de la deuxième formule.
- Interprétations ensemblistes (voir aussi page 25).