Analyse binaire

Transformation des expressions binaires

 Simplification des fonctions binaires
Page suivante

Nous allons examiner maintenant quelques transformations simples que peuvent subir les formes canoniques compte tenu des théorèmes déjà établis.

Transpositions.

Nous avons appelé (2.4) transposition, le passage, pour une même fonction, de la première à la deuxième forme canonique ou réciproquement.

Pour transposer une fonction de « n » variables, mise sous forme canonique, il est recommandé d’écrire pour cette fonction, une table de vérité complète en inscrivant les « 2^n » combinaisons de valeurs des variables dans un ordre binaire naturel.

Si une fonction binaire de « n » variables, mise sous la première forme canonique, contient « p » produits, elle contient nécessairement lorsqu’elle est transposée, « q » produels tels que : p+q=2^n.

Il en résulte que la transposition est un moyen de simplification dans le cas où le nombre de produit ou de produels d’une fonction canonique de « n » variables est supérieur à « 2^{n-1} ».

    \[ f = \begin{array}{|c|} x_{1} . \overline{x}_{2} . \overline{x}_{3} \\ \overline{x}_{1} . x_{2} . \overline{x}_{3} \\ \overline{x}_{1} . \overline{x}_{2} . x_{3} \\ \end{array} \]


Établissement de la deuxième forme canonique


Pour établir la deuxième forme canonique relative aux combinaisons de valeurs de « n » variables pour lesquelles cette fonction est nulle, on inscrit verticalement les variables x_{1}, x_{2},\ldots, x_{n} dans un ordre quelconque et successivement dans le même ordre vertical, les combinaisons de valeurs pour lesquelles f = 0. Il suffit alors d’écrire les produit des produels obtenus en remplaçant respectivement dans ce tableau, chaque valeur « 0 » par la variable « x_{k} » de la même ligne et chaque valeurs « 1 » — par le complément « \overline{x}_{k} » — de la variable de la même ligne.

Exemple :

Établir la deuxième forme canonique d’une fonction de trois variables x_{1}, x_{2}, x_{3}, égale à zéro lorsque deux au moins des trois variables sont égales à l’unité.

La table de vérité s’écrit :


\begin{tabular}{|c|c|c||c|} \hline $x_{1}$ &$x_{2}$ &$x_{3}$ & $f$ \\ \hline 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 0 \\ 1 & 1 & 0 & 0 \\ 1 & 1 & 1 & 0 \\ \hline \end{tabular}
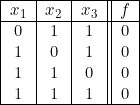
Comme nous l’avons indiqué précédemment, nous en tirons le tableau :

    \[ \begin{array} {c|c|c|c|c|} x_{1} & 0 & 1 & 1 & 1 \\ x_{2} & 1 & 0 & 1 & 1 \\ x_{3} & 1 & 1 & 0 & 1 \\ \end{array} \]


d’où la fonction cherchée :

    \[ f = \begin{array}{|c|c|c|c|} {x}_{1} &\overline{x}_{1} &\overline{x}_{1} &\overline{x}_{1} \\ \overline{x}_{2} &{x}_{2} &\overline{x}_{2} &\overline{x}_{2} \\ \overline{x}_{3} &\overline{x}_{3} &{x}_{3} &\overline{x}_{3} \\ \end{array} \]


Présentation des tables de vérité


Table de vérité complète.


Nous dirons qu’une table de vérité est complète lorsqu’elle fait apparaître la totalité des « 2^{n} » — combinaisons de valeurs possibles, relatives aux « n » — variables dont dépend la fonction.

Nous conviendrons d’inscrire les valeurs (0 ou 1) que prend la fonction à droite d’un double trait vertical de séparation et sur la même ligne que la combinaison correspondante des valeurs des variables.

Ainsi la table de vérité complète d’une fonction de trois variables, F(a, b, c), peut s’écrire par exemple :


\begin{tabular}{r|c|c|c||c|} \multicolumn{1}{c} {} & \multicolumn{4}{c}{\it Table de vérité} \\ \cline{2-5} & a & b & c & F \\ \cline{2-5} 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 1 & 0 \\ 2 & 0 & 1 & 0 & 0 \\ 3 & 0 & 1 & 1 & 0 \\ 4 & 1 & 0 & 0 & 1 \\ 5 & 1 & 0 & 1 & 0 \\ 6 & 1 & 1 & 0 & 1 \\ 7 & 1 & 1 & 1 & 1 \\ \cline{2-5} \end{tabular}

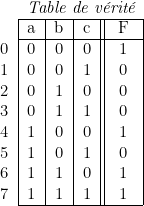
Il est souvent intéressant de faire figurer dans une colonne, à gauche, des repères décimaux qui correspondent aux nombres représentés par les chiffres binaires a, b, c, en plaçant ces nombres dans l’ordre naturel. Cette disposition permet, en particulier, de s’assurer qu’aucune combinaison n’a été oubliée.

Une table de vérité complète autorise, en suivant les règles énoncées précédemment, l’écriture immédiate de la fonction sous ses deux formes canoniques.

En ce qui concerne l’exemple donné, nous pouvons écrire :

    \[ F = \begin{array}{|c|} \overline{a} . \overline{b} . \overline{c}\\ {a} . \overline{b} . \overline{c}\\ {a} . {b} . \overline{c}\\ {a} . {b} . {c}\\ \end{array} = \begin{array}{|c|c|c|c|} a & a & a & \overline{a} \\ b & \overline{b} & \overline{b} & b \\ \overline{c} & c & \overline{c} & \overline{c} \\ \end{array} \]

La première forme utilise les combinaisons pour lesquelles F = 1, (0, 4, 6, 7), et la seconde forme les combinaisons pour lesquelles F = 0, (1, 2, 3, 5).

Tables de vérité incomplètes.

Une fonction binaire est entièrement définie si l’on connaît seulement les combinaisons de valeurs des variables pour lesquelles elle conserve la même valeur (0 ou 1).

Nous appellerons, par définition, table de vérité incomplète, le tableau dans lequel sont inscrites ces combinaisons. Nous préciserons, à droite de ce tableau, la valeur correspondante de la fonction. Pour chaque fonction il existe donc deux tables de vérité incomplètes.

Les deux tables de vérité incomplètes qui correspondent à la fonction précédente F(a, b, c) peuvent s’écrire suivant que l’on choisit pour « F » la valeur « 0 » ou la valeur « 1 » :


\begin{tabular}{l@{\hspace*{3cm}}r} \begin{tabular}{r|c|c|c||c|} \multicolumn{1}{c} {} & \multicolumn{4}{c}{{\it Table de vérité} ($F=1$)} \\ \cline{2-5} & a & b & c & F \\ \cline{2-5} 0 & 0 & 0 & 0 & \multirow{4}{*}{$F=1$} \\ 4 & 1 & 0 & 0 & \\ 6 & 1 & 1 & 0 & \\ 7 & 1 & 1 & 1 & \\ \cline{2-5} \end{tabular} & \begin{tabular}{r|c|c|c||c|} \multicolumn{1}{c} {} & \multicolumn{4}{c}{{\it Table de vérité} ($F=0$)} \\ \cline{2-5} & a & b & c & F \\ \cline{2-5} 1 & 0 & 0 & 1 & \multirow{4}{*}{$F=0$}\\ 2 & 0 & 1 & 0 & \\ 3 & 0 & 1 & 1 & \\ 5 & 1 & 0 & 1 & \\ \cline{2-5} \end{tabular} \end{tabular}


Une table de vérité incomplète ne permet d’écrire que l’une des deux formes canoniques. La propriété de dualité la rend cependant suffisante pour définir complétement une fonction binaire.

Tables de vérité réduites.

Ce sont des tables de vérité incomplète dans lesquelles certaines combinaisons sont groupées afin de tenir compte d’une partie ou de la totalité des adjacences qui existent entre elles. Ces adjacences étant repérées dans la table par le symbole « \phi » qui signifie que la valeur prise par la variable peut être indifféremment « 0 » ou « 1 ». Nous pouvons tirer de l’exemple pfécèdent différentes tables de vérités réduites, parmi lesquelles les deux suivantes :


\begin{tabular}{l@{\hspace*{3cm}}r} \begin{tabular}{r|c|c|c||c|} \cline{2-5} & a & b & c & F \\ \cline{2-5} 0-4 &$\phi$ & 0 & 0 & \multirow{2}{*}{$\big\rbrace F=1$} \\ 6-7 & 1 & 1 & $\phi$ & \\ \cline{2-5} \end{tabular} & \begin{tabular}{r|c|c|c||c|} \cline{2-5} & a & b & c & F \\ \cline{2-5} 1-5 & $\phi$ & 0 & 1 & \multirow{2}{*}{$\big\rbrace F=0$}\\ 2-3 & 0 & 1 & $\phi$ & \\ \cline{2-5} \end{tabular} \end{tabular}


L’adjacence, comme nous le verrons quand nous étudierons les simplifications, a pour effet de supprimer la variable biforme (directe et complémentée) dans le produit ou le produel qui résulte des combinaisons groupées. Une table de vérité réduite ne donne donc plus une forme canonique mais une forme déjà simplifiée. Dans le cas envisagé, nous tirons de la première table de vérité réduite :

    \[ F = \begin{array}{|c|} \overline{b} . \overline{c}\\ {a} . {b} \\ \end{array} \]

De la seconde table de vérité réduite nous tirons :

    \[ F = \begin{array}{|c|c|} {b} & {a} \\ \overline{c} & \overline{b}\\ \end{array} \]

Analyse binaire
 		Simplification des fonctions binaires
Page suivante