Théorèmes, métathéorèmes, règles dérivées

La relation d’implication et celle d’équivalence

Avant d’aller plus loin, faisons le point de ce qui est déjà acquis. Nous sommes partis de propositions atomiques, en ce sens que, pour l’instant, nous renonçons à les analyser plus avant. Ces propositions sont vraies ou fausses et nous les désignons par des minuscules : $p$ , $q$ , $m$ , etc.

Nous nous sommes aussi donnés des foncteurs propositionnels : $\supset$ , $\wedge$ et $\equiv$ qui désignent des opérations. Cela signifie que, placés entre deux propositions (pas nécessairement atomiques d’ailleurs), ils engendrent une nouvelle proposition complexe ou, comme nous l’avons dit aussi, moléculaire.

Exemples. Si nous partons des propositions atomiques $p$ et $q$ , nous pourrons engendrer successivement, par exemple :

(1) $p\wedge q$
(2) $(p\wedge q)\supset p$
(3) $p\supset(p\wedge q)$ .

« Se donner » des foncteurs revenait, dans le présent contexte, à poser des règles pour les introduire et pour les éliminer dans le cours d’une déduction. Il se trouve que, en appliquant les règles, il est parfois possible de déduire une proposition à partir d’une ou de plusieurs autres.

Exemple : La proposition $q$ peut se déduire des deux propositions $p$ et $p\supset q$ . Nous disons aussi que $q$ peut se déduire de la classe d’hypothèses { $p$ , $p\supset q$ } et nous notons : $p$ , $p\supset q\vdash q$ .

Les propositions, qui sont déductibles à partir de la classe d’hypothèses vide, forment un ensemble particulier, celui des théorèmes du système.

Ainsi la proposition (2) ci-dessus est un théorème et nous écrivons : $\vdash(p\wedge q)\supset p$ .

D’autre part, nous avons aussi introduit des majuscules $P$ , $Q$ , $M$ , etc. que nous avons appelées des variables syntaxiques ou encore métavariables.

Elles prennent des propositions (quelconques) comme valeurs. Comment en faire usage ? Pour voir la chose clairement, prenons un exemple.

Soit la proposition (qui d’ailleurs est un théorème) « $\left(p\wedge q\right)\supset p$ ». Rien n’empêche de l’appeler $P$ , donc de donner à la variable $P$ la valeur $\left(p\wedge q\right)\supset p$ . Mais on peut aussi remarquer que la proposition en question est une conditionnelle. Pour souligner la chose, nous pourrions l’écrire sous la forme $P\supset Q$ . Dans ce cas nous attribuons à $P$ la valeur $p\wedge q$ et à $Q$ la valeur $p$ . Nous pourrions aussi songer à souligner le fait que l’antécédent de cette conditionnelle est une conjonction et écrire que la proposition est de la forme $(P\wedge Q)\supset M$ . Dans ce cas, $P$ aurait la valeur $p$ , $Q$ la valeur $q$ et $M$ la valeur $p$ . Enfin, nous pourrions vouloir marquer que le proposition $p$ se retrouve deux fois. Cela nous conduirait à écrire~ : $(P\wedge Q)\supset P$ .
On constate alors que la proposition $\left(p\wedge q\right)\supset p$ et l’expression $(P\wedge Q)\supset P$ ne diffèrent qu’en ce que la première s’écrit avec des minuscules (c’est une proposition du système) et la seconde avec des majuscules. Mais, comme $P$ et $Q$ ne sont pas des propositions, mais des variables, il serait abusif de l’appeler une proposition. Nous dirons qu’il s’agit d’une forme propositionnelle.

Faisons un pas de plus. Dans le cas qui nous occupe, $\left(p\wedge q\right)\supset p$ est un théorème. Nous dirons alors que la forme propositionnelle, que l’on obtient en remplaçant les minuscules par des majuscules, sous les deux conditions suivantes~ :

1) à une même minuscule correspond une même majuscule,
2) à deux minuscules différentes correspondent deux majuscules différentes, est un métathéorème.

Il est ainsi clair que, à chacun des théorèmes que nous avons démontré, on peut faire correspondre un métathéorème.

Exemples

$\begin{tabular}{lcl} {\it Théorèmes} & & {\it Métathéorèmes}\\ $\vdash p\supset p$ & & (1) $\vdash P\supset P$\\ $\vdash\left(p\supset q\right)\wedge\left(q\supset m\right)\cdot\supset\left(p\supset m\right)$ & & (2) $\vdash\left(P\supset Q\right)\wedge\left(Q\supset M\right)\cdot\supset\left(P\supset M\right)$\\ $\vdash\left(p\supset q\right)\wedge\left(q\supset p\right)\cdot\supset\left(p\equiv q\right)$ & & (3) $\vdash\left(P\supset Q\right)\wedge\left(Q\supset P\right)\cdot\supset\left(P\equiv Q\right)$\\ $\vdash p\equiv p$ & & (4) $\vdash P\equiv P$\\ $\vdash p\equiv q\cdot\supset\cdot q\equiv p$ & & (5) $\vdash P\equiv Q\cdot\supset\cdot Q\equiv P$\\ $\vdash(p\equiv q)\wedge(q\equiv m)\cdot\supset(p\equiv m)$ & & (6) $\vdash(P\equiv Q)\wedge(Q\equiv M)\cdot\supset(P\equiv M)$\\ $\vdash p\equiv\cdot p\wedge p$ & & (7) $\vdash P\equiv\cdot P\wedge P$\\ $\vdash p\wedge q\cdot\equiv\cdot q\wedge p$ & & (8) $\vdash P\wedge Q\cdot\equiv\cdot Q\wedge P$\\ $\vdash(p\wedge q)\wedge m\cdot\equiv\cdot p\wedge(q\wedge m)$ & & (9) $\vdash(P\wedge Q)\wedge M\cdot\equiv\cdot P\wedge(Q\wedge M)$\\ \end{tabular}$

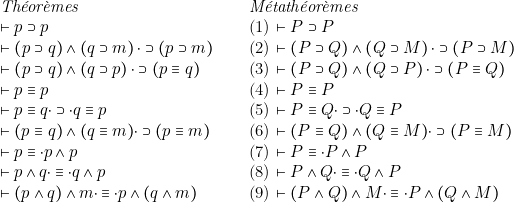
Un métathéorème offre l’avantage de « condenser » en lui un nombre indéfini de théorèmes. Il suffit, pour les écrire, de donner à ses variables des valeurs arbitraires en respectant la condition : à une même variable, attribuer la même valeur.

Exemple : le métathéorème $\vdash P \wedge Q\supset P$ .

$\begin{tabular}{ccccc} Variables & & Valeurs atrtribuées & & Théorèmes\\ $P$ et $Q$ & & $p$ et $q$ & & $\vdash\left(p\wedge q\right)\supset p$\\ $P$ et $Q$ & & $q$ et $p$ & & $\vdash\left(q\wedge p\right)\supset q$\\ $P$ et $Q$ & & $p$ et $p$ & & $\vdash\left(p\wedge p\right)\supset p$\\ $P$ et $Q$ & & $\left(p\wedge q\right)$ et $\left(q\supset p\right)$ & & $\vdash\left(p\wedge q\right)\wedge\left(q\supset p\right)\cdot\supset\left(p\wedge q\right)$\\ \end{tabular}$

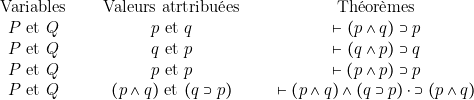
Passons maintenant aux règles. La première chose à laquelle on peut songer, est de les combiner entre elles pour en obtenir de nouvelles, que nous appellerons des règles dérivées. Il est ainsi particulièrement commode de chercher des règles dérivées pour le fondeur $\equiv$ .

$\begin{tabular}{c|lcl} {\small 1} & {\small $P\supset Q$} & & {\small hyp}\\ {\small 2} & {\small $Q\supset P$} & & {\small hyp}\\ \cline{2-2} {\small 3} & \multicolumn{2}{l}{{\small $\left(P\supset Q\right)\wedge\left(Q\supset P\right)$}} & {\small 1, 2, $\wedge$i}\\ {\small 4} & \multicolumn{2}{l}{{\small $P\equiv Q$}} & {\small 3, repdf$\equiv$}\\ \end{tabular}{\small \hfill{}}% \begin{tabular}{c|ll||cl} {\small 1} & \multicolumn{3}{l}{{\small $P\equiv Q$}} & {\small hyp}\\ {\small 2} & {\small $P$} & \multicolumn{2}{l}{} & {\small hyp}\\ \cline{2-2} {\small 3} & \multicolumn{3}{l}{{\small $\left(P\supset Q\right)\wedge\left(Q\supset P\right)$}} & {\small 1, repdf $\equiv$}\\ {\small 4} & \multicolumn{3}{l}{{\small $P\supset Q$}} & {\small 3, $\wedge$e}\\ {\small 5} & \multicolumn{3}{l}{{\small $Q$}} & {\small 2, 3, $\supset$e}\\ \end{tabular}$

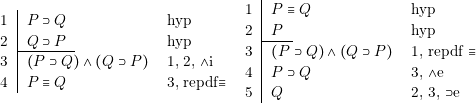
D’où les règles :

$\begin{tabular}{c|lllc} \multicolumn{5}{l}{\textbf{\small Règle $\mathbf{\equiv}$ i}}\\ {\small $n$} & {\small $P\supset Q$} & & & \\ {\small $m$} & \multicolumn{1}{l}{{\small $Q\supset P$}} & & \\ & {\small \ldots{}} & & \multicolumn{2}{l}{}\\ & \multicolumn{1}{l}{{\small $P\equiv Q$}} & & {\small $n$, $m$, $\equiv$i}\\ \end{tabular}\hfill{}{\small }% \begin{tabular}{c|lllc} \multicolumn{5}{l}{\textbf{\small Règle $\mathbf{\equiv}$ e}}\\ {\small $n$} & \multicolumn{2}{l}{{\small $P\equiv Q$}} & & \\ {\small $m$} & \multicolumn{1}{l}{{\small $P$}} & & \\ & {\small \ldots{}} & & \multicolumn{2}{l}{}\\ & \multicolumn{1}{l}{{\small $Q$}} & \multicolumn{3}{l}{{\small $n$, $m$, $\equiv$e}}\\ \end{tabular}\hfill{}{\small }% \begin{tabular}{c|lllc} \multicolumn{5}{l}{}\\ {\small $n$} & \multicolumn{2}{l}{{\small $P\equiv Q$}} & & \\ {\small $m$} & \multicolumn{1}{l}{{\small $Q$}} & & \\ & {\small \ldots{}} & & \multicolumn{2}{l}{}\\ & \multicolumn{1}{l}{{\small $P$}} & \multicolumn{3}{l}{{\small $n$, $m$, $\equiv$e}}\\ \end{tabular}$

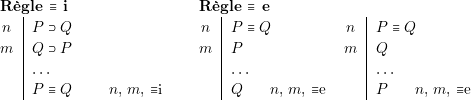
Remarque

La seconde règle d’élimination s’obtient de façon analogue à la première.

Mais on peut faire encore plus. Nos règles ont certaines propriétés que l’on peut étudier, ou mieux, dont on peut étudier les effets. Expliquons-nous sur un exemple.

Supposons qu’on ait pu démontrer deux métathéorèmes, disons $\vdash P^{'}$ et $\vdash P^{'}\supset Q^{'}$ . Cela signifie que nos règles nous ont permis de déduire, à partir de la classe d’hypothèses vide deux expressions de la forme $P^{'}$ et $P^{'}\supset Q^{'}$ . Dans ces conditions, elles nous permettraient aussi de déduire l’expression $Q^{'}$ de la classe d’hypothèses vide. Pour s’en assurer, il suffit de raisonner de la façon suivante :

1) Puisque $\vdash P^{'}$ , c’est qu’on peut trouver une démonstration de $P^{'}$ , disons en $m$ étapes,
2) De même, puisque $\vdash P^{'}\supset Q^{'}$ , c’est qu’on peut trouver
une démonstration de $P^{'}\supset Q^{'}$ , disons en $n$ étapes,
3) Mettons ces deux démonstrations bout à bout et poursuivons comme il est indiqué :

$\setbox1=\vbox{\hsize=0.4cm \begin{tabular}{r} l \\ \\ \\ m \\ \end{tabular}} \setbox2=\vbox{\hsize=2cm \begin{tabular}{l} $\cdot$ \\ $\cdot$ \\ $\cdot$ \\ $P'$\\ \end{tabular}} \setbox3=\vbox{\hsize=1cm \[\left. \begin{tabular}{c} \\ \\ \\ \\ \end{tabular} \right\} \text{Démonstration de $P'$} \] } \setbox4=\vbox{\hsize=1cm \begin{tabular}{r} $m+1$\\ \\ \\ $m+n$ \\ \end{tabular}} \setbox5=\vbox{\hsize=2cm \begin{tabular}{l} $\cdot$ \\ $\cdot$ \\ $\cdot$ \\ $P'\supset Q'$\\ \end{tabular}} \setbox6=\vbox{\hsize=1cm \[\left. \begin{tabular}{c} \\ \\ \\ \\ \end{tabular} \right\} \text{Démonstration de $P'\supset Q'$} \] } \begin{tabular}{r|ll} $\vcenter{\box1}$&$\vcenter{\box2}$&$\vcenter{\box3}$\\ $\vcenter{\box4}$&$\vcenter{\box5}$&$\vcenter{\box6}$\\ &~~$Q'$ & $m$, $m+n$, $\supset$ e\\ \end{tabular}$

On a donc bien, sous les deux conditions $\vdash P^{'}$ et $\vdash P^{'}\supset Q^{'}$ , que $Q'$ est un métathéorème, donc que $\vdash Q^{'}$ .

Cette constatation porte sur une propriété de notre système. On peut l’énoncer en disant :

Si $P'$ est un théorème dans le système et si $P^{'}\supset Q^{'}$ , en est aussi un, alors $Q'$ est un théorème dans le système.

Nous appellerons épithéorèmes des énoncés de ce genre, qui portent sur la logique que nous construisons. Et nous écrirons~ :

Épithéorème 1 : $\vdash P^{'}$ et $\vdash P^{'}\supset Q^{'}\Longrightarrow Q'$

Remarque

Le signe $\Longrightarrow$ n’appartient pas au système, pas plus que « et » ou que $\vdash$ . Il abrège un discours sur le système et est donc un métasigne.

Exemple d’application

Prenons pour $P'$ l’expression $P\equiv Q$ et pour $Q'$ l’expression $Q\equiv P$ . Nous savons que $\vdash P\equiv Q\cdot\supset\cdot Q\equiv P$ (métathéorème (5) de tout à l’heure). Nous pouvons donc dire :

({*}) Si $\vdash P\equiv Q$ alors $\vdash Q\equiv P$ .

En effet, l’épithéorème 1 suppose deux conditions :

1) $\vdash P^{'}$ , donc ici que $P\equiv Q$ soit un métathéorème,
2) $P^{'}\supset Q^{'}$ , donc ici que $P\equiv Q\cdot\supset\cdot Q\equiv P$ soit aussi un métathéorème.

Mais cette seconde condition est établie. Il ne reste donc plus que la condition (1). D’où l’énoncé ({*}) que nous pouvons écrire en abrégé~ :

$\vdash P\equiv Q\;\Longrightarrow\;\vdash Q\equiv P$

Remarque

Il est très important de noter que, si les raisonnements qui permettent d’établir et d’utiliser un épithéorême se font « logiquement », il ne saurait être question de les faire dans notre système. Nous sommes obligés de faire appel aux pratiques non formelles de la pensée naturelle.

Donnons encore un second exemple, qui sera utile plus loin.

Épithéorème 2 : $\vdash P'$ , $\vdash Q'$ , $\vdash\left(P'\wedge Q'\right)\supset M'\;\Longrightarrow\;\vdash M'$

Le raisonnement est analogue au précédent et nous nous bornons à l’indiquer~ :

$\setbox1=\vbox{\hsize=.4cm \begin{tabular}{r} l \\ \\ \\ m \\ \end{tabular}} \setbox2=\vbox{\hsize=2cm \begin{tabular}{l} $\cdot$ \\ $\cdot$ \\ $\cdot$ \\ $P'$\\ \end{tabular}} \setbox3=\vbox{\hsize=1cm \[\left. \begin{tabular}{c} \\ \\ \\ \\ \end{tabular} \right\} \text{Démonstration de $P'$} \] } \setbox4=\vbox{\hsize=1cm \begin{tabular}{r} $m+1$\\ \\ \\ $m+n$ \\ \end{tabular}} \setbox5=\vbox{\hsize=2cm \begin{tabular}{l} $\cdot$ \\ $\cdot$ \\ $\cdot$ \\ $P'\supset Q'$\\ \end{tabular}} \setbox6=\vbox{\hsize=1cm \[\left. \begin{tabular}{c} \\ \\ \\ \\ \end{tabular} \right\} \text{Démonstration de $Q'$} \] } %%%%%%%%%%%%%%%%%%%%%%%%% \setbox7=\vbox{\hsize=1.6cm \begin{tabular}{r} $m+n+1$\\ \\ \\ $m+n+1$ \\ \end{tabular}} \setbox8=\vbox{\hsize=2cm \begin{tabular}{l} $\cdot$ \\ $\cdot$ \\ $\cdot$ \\ $P'\wedge Q' \supset M'$\\ \end{tabular}} \setbox9=\vbox{\hsize=1cm \[\left. \begin{tabular}{c} \\ \\ \\ \\ \end{tabular} \right\} \text{Démonstration de $P'\wedge Q' \supset M'$} \] } \begin{tabular}{r|ll} $\vcenter{\box1}$&$\vcenter{\box2}$&$\vcenter{\box3}$\\ $\vcenter{\box4}$&$\vcenter{\box5}$&$\vcenter{\box6}$\\ $\vcenter{\box7}$&$\vcenter{\box8}$&$\vcenter{\box9}$\\ m+n+k+1&~~$p'\wedge Q'$ & $m$, $m+n$, $\wedge$ i\\ m+n+k+2&~~$M'$ & $m+n+k$, $m+n+k+1$, $\supset$ e\\ \end{tabular}$