Quelques propriétés de la logique des propositions |
Après qu’on a construit un logique, et plus généralement un système formel quelconque, il convient d’en dégager les principales propriétés. Celles-ci doivent naturellement être démontrées. Elles font alors l’objet de théorèmes qui portent sur le système : nous les appellerons des épithéorèmes. Démontrer un épithéorème exige de disposer de certains moyens logiques. S’ils se veulent rigoureux, ceux-ci ne sont pas élémentaires et dépassent le cadre de cet ouvrage. Nous allons cependant énoncer un certain nombre d’épithéorèmes relatifs à la logique des propositions et en esquisser des preuves simples.
Remarquons d’abord que nous avons affaire à deux notions de théorèmes. Au fascicule I, nous avons dit qu’un théorème était une expression qui pouvait se déduire, par les règles du système, de la classe d’hypothèses vide. Si ![]() est un théorème en ce sens, nous noterons provisoirement
est un théorème en ce sens, nous noterons provisoirement ![]() . Par ailleurs, nous venons de donner une autre définition de la notion de théorème. Si
. Par ailleurs, nous venons de donner une autre définition de la notion de théorème. Si ![]() est un théorème en ce second sens, nous écrirons
est un théorème en ce second sens, nous écrirons ![]() . La question qui se pose est de savoir, non pas si les deux notions sont les mêmes (en fait, elles sont formulées différemment), mais si la classe des théorèmes au sens 1 est la même que celle des théorèmes au sens 2. Comme, par définition, deux classes sont égales si elles contiennent les mêmes éléments, il suffit de se demander si, chaque fois que l’on a
. La question qui se pose est de savoir, non pas si les deux notions sont les mêmes (en fait, elles sont formulées différemment), mais si la classe des théorèmes au sens 1 est la même que celle des théorèmes au sens 2. Comme, par définition, deux classes sont égales si elles contiennent les mêmes éléments, il suffit de se demander si, chaque fois que l’on a ![]() on a aussi
on a aussi ![]() et réciproquement. La réponse à cette question est affirmative.
et réciproquement. La réponse à cette question est affirmative.
Epithéorème 1 : ![]() si et seulement si
si et seulement si![]() .
.
La preuve doit être double. Il faut montrer :
I. Si ![]() alors
alors ![]() .
.
II. Si ![]() alors
alors ![]() .
.
Commençons par esquisser la preuve de II. Dire que ![]() , c’est dire que l’on a pu obtenir
, c’est dire que l’on a pu obtenir ![]() à partir d’axiomes en appliquant la règle (R1). Or il est facile de montrer que les trois schémas d’axiomes sont des métathéorèmes au sens 1 (V. I, p. 22). Il suffit, par exemple, d’écrire avec des majuscules la déduction de l’exemple 2 de la page 15 (Fascicule I), pour obtenir (A1). D’autre part, la règle (R1) n’est rien d’autre que la règle
à partir d’axiomes en appliquant la règle (R1). Or il est facile de montrer que les trois schémas d’axiomes sont des métathéorèmes au sens 1 (V. I, p. 22). Il suffit, par exemple, d’écrire avec des majuscules la déduction de l’exemple 2 de la page 15 (Fascicule I), pour obtenir (A1). D’autre part, la règle (R1) n’est rien d’autre que la règle ![]() e. Donc, tout ce qui sera théorème au sens 2, le sera au sens 1.
e. Donc, tout ce qui sera théorème au sens 2, le sera au sens 1.
Esquissons maintenant la preuve de I. Nous avons vu qu’il était possible, dans le cadre de l’axiomatique précédente, de déduire des règles à partir des schémas d’axiomes. Il est clair que l’on peut procéder de même à partir de schémas de théorèmes ou métathéorèmes. Supposons, ce qui est le cas mais que nous ne démontrerons pas, que l’on ait :
![]() .
.
On aura immédiatement, par une double application de (R1) : ![]() ,
, ![]() , ce qui n’est qu’une autre écriture pour la règle
, ce qui n’est qu’une autre écriture pour la règle ![]() i.
i.
En conséquence de ce premier épithéorème, nous écrirons dès maintenant ![]() pour dire que
pour dire que ![]() est un théorème, aussi bien au sens 1 qu’au sens 2.
est un théorème, aussi bien au sens 1 qu’au sens 2.
Examinons les relations entre la classe des théorèmes et celle des tautologies et, pour cela, notons provisoirement par ![]() , le fait que
, le fait que ![]() est une tautologie. Nous avons tout d’abord :
est une tautologie. Nous avons tout d’abord :
Epithéorème 2 : Si ![]() , alors
, alors ![]() .
.
Dire que ![]() , c’est dire que
, c’est dire que ![]() a son origine dans un ou plusieurs axiomes. Mais, il est aisé de s’assurer que tous les axiomes du système sont des tautologies. En effet, quelles que soient les propositions
a son origine dans un ou plusieurs axiomes. Mais, il est aisé de s’assurer que tous les axiomes du système sont des tautologies. En effet, quelles que soient les propositions ![]() ,
, ![]() et
et![]() , elles seront dans notre interprétation, vraies ou fausses. On aura donc pour (Al) par exemple :
, elles seront dans notre interprétation, vraies ou fausses. On aura donc pour (Al) par exemple :
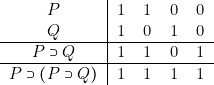
De plus, si![]() , il est engendré à partir d’axiomes qui sont des tautologies, par la seule règle (R1). Or celle-ci conserve, si l’on peut dire, la vérité. En effet, ses deux prémisses
, il est engendré à partir d’axiomes qui sont des tautologies, par la seule règle (R1). Or celle-ci conserve, si l’on peut dire, la vérité. En effet, ses deux prémisses ![]() et
et ![]() sont des tautologies. Considérons alors la table de
sont des tautologies. Considérons alors la table de ![]() :
:
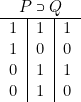
|
Sa deuxième ligne est exclue par la condition |
|
L’épithéorème 2 a deux corollaires importants.
Définition. Un système formel, dont un signe, disons ![]() , est interprété comme la négation est non contradictoire, s’il est impossible d’y démontrer à la fois
, est interprété comme la négation est non contradictoire, s’il est impossible d’y démontrer à la fois ![]() et
et ![]() .
.
Corollaire 1. La logique des propositions est non contradictoire.
Supposons, en effet, que ![]() . Alors, par l’épithéorème 2, on
. Alors, par l’épithéorème 2, on ![]() . Il s’ensuit que
. Il s’ensuit que ![]() n’a que que des 0 dans son évaluation et que
n’a que que des 0 dans son évaluation et que ![]() , c’est-à-dire que
, c’est-à-dire que ![]() n’est pas une tautologie. Par contraposition, l’épithéorème 2, montre que
n’est pas une tautologie. Par contraposition, l’épithéorème 2, montre que ![]() , donc que
, donc que ![]() n’est pas un théorème.
n’est pas un théorème.
Remarque
La contraposée d’un théorème de la forme « si ![]() alors
alors ![]() » est l’expression « si
» est l’expression « si ![]() alors
alors ![]() ». Les deux formes sont logiquement équivalentes.
». Les deux formes sont logiquement équivalentes.
La définition de la non-contradiction exige que le système soit interprété. Qu’en est-il des systèmes purement formels ? Pour faire face à ce problème, on pose :
Définition. Un système est consistant, s’il possède au moins une ebf qui n’est pas un théorème.
Corollaire 2. Le système de la logique des propositions est consistant.
En effet, nous avons vu que ![]() . Par l’épithéorème 2, on
. Par l’épithéorème 2, on ![]() . En conséquence
. En conséquence ![]() et par la contraposée de l’épithéorème,
et par la contraposée de l’épithéorème, ![]() est un exemple d’ebf qui n’est pas un théorème.
est un exemple d’ebf qui n’est pas un théorème.
Remarque
On peut prouver que si un système est non contradictoire, il est toujours consistant, mais que la réciproque n’est pas vraie. La condition de noncontradiction est donc « plus forte » que celle de consistance.
Epithéorème 3 : Si ![]() alors
alors ![]() .
.
La marche de la preuve, qui est assez longue, est la suivante :
1) Démontrer que si ![]() est la fnc de
est la fnc de ![]() , on a le métathéorème
, on a le métathéorème ![]() .
.
2) Si ![]() alors chacune de ses disjonctions est aussi une tautologie. Si l’une d’elles ne l’était pas, il se pourrait en effet que la conjonction ne soit pas toujours vraie.
alors chacune de ses disjonctions est aussi une tautologie. Si l’une d’elles ne l’était pas, il se pourrait en effet que la conjonction ne soit pas toujours vraie.
3) Démontrer ![]() . Comme on a la règle dérivée
. Comme on a la règle dérivée ![]() , toute disjonction élémentaire sera un théorème. Mais comme on a aussi la règle dérivée
, toute disjonction élémentaire sera un théorème. Mais comme on a aussi la règle dérivée ![]() ,
, ![]() , toute fnc tautologique sera un théorème. Donc
, toute fnc tautologique sera un théorème. Donc ![]()
4) Démontrer que ![]() . Alors, par les points (1), (3) et (R1), il vient
. Alors, par les points (1), (3) et (R1), il vient ![]() .
.
Cet épithéorème a aussi deux corollaires importants.
Définition. Un système interprété est complet au sens faible, si l’on peut y démontrer toutes les ebf qui correspondent à des vérités dans l’interprétation choisie.
Corollaire 1. Si l’on considère que toute tautologie est une vérité logique, le calcul des propositions est complet au sens faible.
L’épithéorème 3 dit, en effet, que toute tautologie est un théorème.
Mais il est de nouveau possible d’introduire une notion de complétude qui n’exige pas d’interpréter le système.
Définition. Un système est complet au sens fort, si l’adjonction à ses schémas d’axiomes d’un schéma d’ebf qui n’y est pas démontrable, le rend inconsistant.
Corollaire 2. Le système de la logique des propositions est complet au sens fort.
Soit en effet, un schéma d’ebf ![]() qui n’est pas démontrable. Posons (A4)
qui n’est pas démontrable. Posons (A4)![]() . Soit de nouveau
. Soit de nouveau ![]() la \textsc{fnc} de
la \textsc{fnc} de ![]() . Nous aurons
. Nous aurons ![]() et par (A4) et (R1), il viendra
et par (A4) et (R1), il viendra ![]() et par l’épithéorème 3,
et par l’épithéorème 3, ![]() est une tautologie. Par ailleurs, puisque par hypothèse
est une tautologie. Par ailleurs, puisque par hypothèse ![]() ,
, ![]() doit contenir au moins une disjonction qui ne contient pas un atome et sa négation, disons qui ne contient pas
doit contenir au moins une disjonction qui ne contient pas un atome et sa négation, disons qui ne contient pas ![]() et
et ![]() . Soit
. Soit ![]() =df
=df ![]() cette disjonction.
cette disjonction.
Comme on a la règle dérivée ![]() on aura en particulier
on aura en particulier ![]() (
(![]() est une conjonction qui, entre autres facteurs, contient
est une conjonction qui, entre autres facteurs, contient ![]() ). Et comme on a
). Et comme on a ![]() , par (R1) on a
, par (R1) on a ![]() , soit
, soit ![]() . Les
. Les ![]() (
(![]() = 1, 2, …,
= 1, 2, …, ![]() ) sont soit des atomes, soit la négation d’un atome.
) sont soit des atomes, soit la négation d’un atome.
Si ![]() est un atome qui n’est pas précédé d’une négation, substituons-lui
est un atome qui n’est pas précédé d’une négation, substituons-lui ![]() . Si
. Si ![]() est un atome précédé d’une négation, substituons-lui
est un atome précédé d’une négation, substituons-lui ![]() . En éliminant les doubles négations, on aura
. En éliminant les doubles négations, on aura ![]() et donc
et donc ![]() .
.
Un raisonnement analogue montre qu’on peut aussi obtenir ![]() . En conséquence le système est contradictoire. Mais il est aussi inconsistant, par la règle :
. En conséquence le système est contradictoire. Mais il est aussi inconsistant, par la règle : ![]() ,
, ![]() .
.
Remarque
La terminologie utilisée laisse entendre, ce qu’on peut démontrer, qu’un système peut être complet au sens faible sans l’être au sens fort (V. 2.4).
Si l’on réunit les épithéorèmes 2 et 3, on est conduit à :
Epithéorème 4 : ![]() si et seulement si
si et seulement si ![]() .
.
Il en découle aussi un corollaire intéressant.
Définition. Un système est décidable si, étant donné une de ses ebf quelconque, il existe un algorithme qui permet de décider si cette ebf est un théorème du système ou non.
Corollaire. Le système de la logique des propositions est décidable.
L’algorithme est le suivant. Soit ![]() l’ebf donnée, on calcule son évaluation.
l’ebf donnée, on calcule son évaluation.
Si elle ne contient que des 1, alors ![]() et
et ![]() . Sinon
. Sinon ![]() et
et ![]() .
.
Remarques
1. Nous avons donné trois présentations de la logique des propositions : par les règles de déduction, par les tables de vérité et par une axiomatisation. Les tables de vérité fournissent les manipulations les plus aisées. Malheureusement, elles ne peuvent s’étendre à la logique des prédicats. C’est la présentation axiomatique qui conduit aux manipulations les plus difficiles. Il y faut souvent beaucoup de pratique et d’imagination. C’est toutefois elle qui se prête le mieux à la réflexion sur la logique. Enfin la méthode de la déduction naturelle est celle qui est généralisable et qui semble la plus commode à utiliser.
2. Les raisonnements de ce paragraphe manquent de rigueur. Il ne faut les tenir que pour des indications, propres tout au plus à faire pressentir le genre de démarches auxquelles conduit ce qu’on appelle la métalogique (V. la bibliographie).
