Règles générales |
Les règles de déduction doivent pouvoir s’appliquer à n’importe quelles propositions, atomiques ou composées. Nous n’allons donc pas les formuler en utilisant des propositions particulières comme « le ciel est couvert » ou « il ne gèle pas », même si celles-ci sont abrégées par des lettres ![]() et
et ![]() . De même qu’en algèbre on utilise des variables,
. De même qu’en algèbre on utilise des variables, ![]() ,
, ![]() , etc., pour désigner des nombres et que celles-ci ne sont pas des nombres, de même nous allons introduire des variables pour désigner des propositions. Nous utiliserons des majuscules :
, etc., pour désigner des nombres et que celles-ci ne sont pas des nombres, de même nous allons introduire des variables pour désigner des propositions. Nous utiliserons des majuscules : ![]() ,
, ![]() ,
, ![]() et ces mêmes lettres affectées d’accents
et ces mêmes lettres affectées d’accents ![]() ,
, ![]() , etc. Ces lettres prennent leurs valeurs sur l’ensemble des propositions, ce qui signifie qu’elles désignent des propositions, atomiques ou composées, sans être elles-mêmes des propositions. On les nomme variables syntaxiques ou métavariables.
, etc. Ces lettres prennent leurs valeurs sur l’ensemble des propositions, ce qui signifie qu’elles désignent des propositions, atomiques ou composées, sans être elles-mêmes des propositions. On les nomme variables syntaxiques ou métavariables.
Exemple : Dans la déduction du paragraphe précédent, ![]() pourrait prendre la valeur « si
pourrait prendre la valeur « si ![]() alors
alors ![]() et si
et si ![]() alors
alors ![]() »,
», ![]() la valeur
la valeur ![]() et
et ![]() la valeur
la valeur ![]() .
.
Remarque
Si une même métavariable figure plusieurs fois dans un contexte donné, il est entendu qu’elle désigne chaque fois la même proposition. En revanche, deux métavariables différentes peuvent désigner soit deux propositions différentes, soit la même proposition.
Règle hyp
Toute déduction part d’une classe de prémisses et on ne voit pas ce qui limiterait la liberté qu’a l’esprit de considérer n’importe quelles propositions pour en examiner les conséquences. Nous allons donc nous donner le droit de poser, sans restrictions, des hypothèses quelconques. Toutefois, il faut savoir exactement de quelles hypothèses dépend la déduction. On peut imaginer toutes sortes de procédés pour ne pas l’oublier. Celui adopté ici, un trait vertical qui court tout au long de la déduction et une petite barre horizontale sous la dernière hypothèse, est emprunté à F. B. Fitch et il se révèle particulièrement commode. Aussi allons-nous poser la règle suivante :
Règle hyp : On peut, à toute étape d’une déduction, introduire une ou plusieurs hypothèses, à condition de les accompagner d’un trait vertical à gauche et de faire suivre la dernière d’une petite barre horizontale.
Exemple :
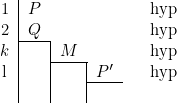
Les nombres 1, 2, …, ![]() ,
, ![]() qui figurent à gauche servent à numéroter les lignes de la déduction. Pas plus que l’abréviation « hyp », qui indique au nom de quelle règle la proposition est posée, ils n’appartiennent à la déduction. Ce sont des indications à soi-même
qui figurent à gauche servent à numéroter les lignes de la déduction. Pas plus que l’abréviation « hyp », qui indique au nom de quelle règle la proposition est posée, ils n’appartiennent à la déduction. Ce sont des indications à soi-même
ou au lecteur.
Règle rep
Toute déduction exige d’écrire des propositions les unes à la suite des autres et se déroule donc dans le temps. Il s’agit toutefois là d’un aspect matériel et contingent. En fait, la déduction elle-même a un caractère atemporel, ce qui fait que toute proposition, une fois posée, le reste tout au long de la déduction.
Nous tiendrons compte de ce double fait – une proposition vraie le reste, mais nous sommes obligés de procéder dans le temps – en nous accordant le droit de répéter, n’importe où dans la déduction toute proposition qui la précède. Et nous noterons :
Règle rep (règle de répétition) :
![]()
Dans le langage quotidien, cette règle correspond à des locutions telles que « comme on l’a vu plus haut », « mais on sait que », etc.
Règle reit
Nous ne voulons pas, ici, limiter le droit à la répétition. Toutefois d’un point de vue formel, nous pouvons nous trouver en présence de deux situations distinctes. Soit la déduction suivante :
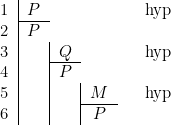
La proposition ![]() a été « répétée » trois fois : lignes 2, 4 et 6. Aux lignes 4 et 6, elle est « répétée » à l’intérieur d’une sous-déduction de la déduction principale, mais à la ligne 2 elle est « répétée » dans la déduction principale elle-même. On peut dire aussi que pour écrire
a été « répétée » trois fois : lignes 2, 4 et 6. Aux lignes 4 et 6, elle est « répétée » à l’intérieur d’une sous-déduction de la déduction principale, mais à la ligne 2 elle est « répétée » dans la déduction principale elle-même. On peut dire aussi que pour écrire ![]() aux lignes 4 et 6, il a fallu franchir une (ou plus d’une) barre verticale, ce qui n’est pas le cas pour la ligne 2. Pour des raisons qui apparaîtront dans la deuxième partie de ce fascicule, il est utile de distinguer les deux cas. Nous parlerons de répétition (règle rep) à la ligne 2 et de réitération aux lignes 4 et 6 (règle reit).
aux lignes 4 et 6, il a fallu franchir une (ou plus d’une) barre verticale, ce qui n’est pas le cas pour la ligne 2. Pour des raisons qui apparaîtront dans la deuxième partie de ce fascicule, il est utile de distinguer les deux cas. Nous parlerons de répétition (règle rep) à la ligne 2 et de réitération aux lignes 4 et 6 (règle reit).
Règle reit :
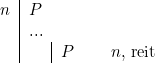
Règle repdf
Il est très souvent commode, et même pratiquement indispensable, d’abréger certaines expressions. Ainsi, au lieu de « lieu géométrique des points équidistants d’un point fixe » est-il usuel de dire « circonférence ». Le mot « circonférence » abrège l’expression « lieu géométrique… », il a la même signification. « Circonférence » est le défini et « lieu géométrique… » est le définissant. Nous désignerons par le signe complexe, mais qui doit être considéré comme un tout, =df la relation qui unit le défini et le définissant.
Exemples :
![]()
Nous nous donnerons alors la règle de répétition par définition sous les deux formes suivantes :
\textbf{Règle repdf}
Si ![]() =df
=df ![]() :
:
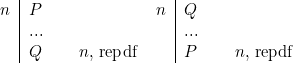
Remarque
![Rendered by QuickLaTeX.com \begin{tabular}{|c} \begin{minipage}[t]{5cm}% Cette règle correspond aux expressions courantes « en d'autres termes », « plus simplement », etc. % \end{minipage}\tabularnewline \end{tabular}](https://jr01.dhenin.fr/wp-content/ql-cache/quicklatex.com-f3ed0dcd8899a54410155be7c9811408_l3.png)
Nous avons dit qu’à ce niveau d’analyse, nous aurions affaire à des propositions considérées comme des touts et reliées entre elles par des conjonctions ou des locutions conjonctives. Ainsi nous nous trouverons en présence d’expressions de la forme : ![]() ,
, ![]() ,
, ![]() et
et ![]() ,
, ![]() ou
ou ![]() , si
, si ![]() alors
alors ![]() , pour prendre quelques exemples.
, pour prendre quelques exemples.
Toute proposition de ce genre peut nous servir d’hypothèse (règle hyp) et être répétée de diverses façons (règles rep, reit, repdf). Ceci est toutefois bien insuffisant pour obtenir des déductions qui pourront s’interpréter de façon utile. Nous devons encore apprendre à composer les propositions entre elles et, lorsqu’elles sont complexes (ou moléculaires) à les décomposer. Nous allons donc chercher deux catégories de règles :
1. Des règles d’introduction qui permettront d’introduire dans les conclusions certains signes de liaison qui ne figuraient pas dans les prémisses.
Exemple : Une de nos règles posera \eqref{sec :La-proposition-conjonctive} qu’à partir des deux prémisses ![]() ,
, ![]() , nous avons le droit de poser la conclusion :
, nous avons le droit de poser la conclusion : ![]() et
et ![]() . La règle aura introduit la conjonction « et ».
. La règle aura introduit la conjonction « et ».
2. Des règles d’élimination qui permettront d’éliminer certaines liaisons qui figuraient dans les prémisses.
Exemple : Une de nos règles posera \eqref{sec :La-proposition-conditionnelle} qu’à partir des deux prémisses ![]() et si
et si ![]() alors
alors ![]() , nous sommes en droit d’écrire la conclusion
, nous sommes en droit d’écrire la conclusion ![]() . La règle aura éliminé la locution « si … alors ».
. La règle aura éliminé la locution « si … alors ».
