I-8. Algèbre de Boole pour trois propositions

De plus en plus fort...

 Systèmes de numération
Page suivante

  • Puisque l’ordinateur J. R. 01 travaille, et joue, avec trois informations, ce qui précède suffit pour aborder la deuxième partie de ce livret.

    Mais qui n’aura pas la curiosité de connaître…la suite.

    Que peut-on dire avec n informations ?

    • — D’abord, combien la table de valeur associée à 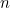n propositions a-t-elle
      de lignes ?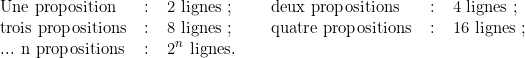

      \begin{tabular}{lclclcl} Une proposition & : & 2 lignes ; & & deux propositions & : & 4 lignes ;\\ trois propositions & : & 8 lignes ; & & quatre propositions & : & 16 lignes ;\\ ... n propositions & : & 2$^{n}$ lignes. & & & & \\ \end{tabular}

    • — Dans chaque ligne, on place, de façon arbitraire, un 1 ou un 0. Quel est le nombre de ces façons ?

      Si nous avons 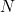N cases dans lesquelles il faut placer un 1 ou un 0, le nombre de possibilités est 2^{N}.

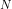      Or ici N=2^{n}.

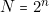      Donc :

      avec n propositions, on peut tenir 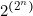2^{(2^{n})} « discours » différents.

      Ainsi :

      \begin{tabular}{rcrcl} -- si {\bf n} = 2, & & $2^{2}=4$, & & $2^{2^{n}}=2^{4}=16$ (§ 5)\\ -- si {\bf n} = 2, & & $2^{3}=8$, & & $2^{2^{n}}=2^{8}=256$ (§7)\\ -- si {\bf n} = 2, & & $2^{4}=16$, & & $2^{16}=65.536$\\ -- si {\bf n} = 2, & & $2^{5}=32$, & & $2^{32}=4.294.967.296$ \\ \end{tabular}

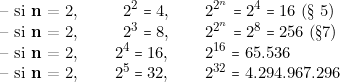
      avec 5 informations, « il y a plus de 4 milliards de possibilités de réponses ».

I-8. Algèbre de Boole pour trois propositions
 		Systèmes de numération
Page suivante