Systèmes de numération

Généralités

Il est aisé, connaissant la base du système de numération utilisé, d’exprimer un nombre dans un autre système. Il suffit pour cela d’exprimer les chiffres et les poids dans le système de numération choisi.

Exemples :

— dans le système à base « six » $(0, 1, 2, 3, 4, 5)$ le nombre « 324 » est représenté en décimal par :

$3 \times (6)^{2} + 2 \times (6) + 4 = 124$

— transposons le nombre $3243312_{5}$ dans le système hexadécimal (base 16), en passant par le système décimal.

$\begin{eqnarray*} 3243312_{5} & = & 3\times(5)^{6}+2\times(5)^{5}+4\times(5)^{4}+3\times(5)^{3}+3\times(5)^{2}+1\times(5)+2 \\ & = & 56082_{10} \\ \end{eqnarray*}$

Pour calculer la valeur en base 16, on effectue les divisions successives par « 16 » du nombre décimal :

$\begin{tabular}{lrrr} 56082 & \multicolumn{1}{|l}{16} & & \\ \cline{2-2} 080 & 3505 & \multicolumn{1}{|l}{16} & \\ \cline{3-3} 00082 & \multicolumn{1}{l}{030} & 219 & \multicolumn{1}{|l}{16} \\ \cline{4-4} 000(2) & 145 & 059 & (13) \\ & 0(1) & (11) & (D) \\ & & (B) & \\ \end{tabular}$

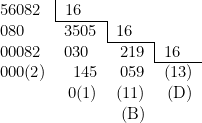
D’où ${\rm 3243312}_{5}={\rm DB12}_{16}$

Numération binaire

La correspondance entre nombres binaires et décimaux s’établit aisément selon les tableaux suivants :

$\begin{tabular}{|r|r|c|lcr|r|} \cline{1-2} \cline{4-7} \multicolumn{1}{|c|}{\em décimal} & \multicolumn{1}{|c|}{\em binaire} & & \multicolumn{3}{|c|}{\em décimal} & \multicolumn{1}{|c|}{\em binaire} \\ \cline{1-2} \cline{4-7} 1 & 1 & & & & 2 & 10 \\ 2 & 10 & & $2^{2}$ & = & 4 & 100 \\ 3 & 11 & & $2^{3}$ & = & 8 & 1000 \\ 4 & 100 & & $2^{4}$ & = &16 & 10000 \\ 5 & 101 & & $2^{5}$ & = &32 & 100000 \\ 6 & 110 & & $2^{6}$ & = &64 & 1000000 \\ 7 & 111 & & $2^{7}$ & = &128 & 10000000 \\ 8 & 1000 & & $2^{8}$ & = &256 & 100000000 \\ 9 & 1001 & & $2^{9}$ & = &512 & 1000000000 \\ 10 & 1010 & & $2^{10}$ & = &1024 & 10000000000 \\ 11 & 1011 & & $2^{11}$ & = &2048 & 100000000000 \\ 12 & 1100 & & $2^{12}$ & = &4096 & 1000000000000 \\ 13 & 1101 & & & & & \\ 14 & 1110 & & & & & \\ 15 & 1111 & & & & & \\ 16 & 10000 & & & & & \\ \cline{1-2} \cline{4-7} \end{tabular}$

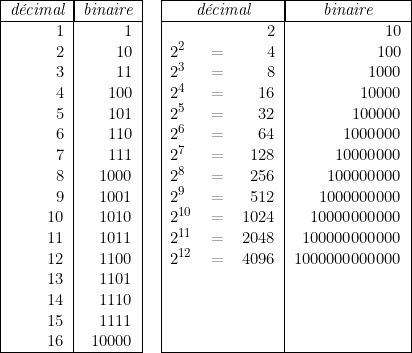
Pour passer d’un nombre binaire, au même nombre exprimé dans le système à base $b = (2)^{n}$ , on groupe les chiffres binaires $n$ par $n$ en partant de la droite, puis on remplace chacun des groupes obtenus à la place qu’il occupe par le chiffre du système à base $(2)^{n}$ qui lui correspond.