Notice 12En rang par trois ou... le jeu du trio |
- 1° Analyse du problème.L’adversaire de l’ordinateur J. R. 01 a, au cours du jeu, 8 possibilitésdifférentes de jouer, à savoir :
- placer sa première pièce (une façon) ;
- placer sa deuxième pièce (deux façons : case voisine de la pièce deJ. R.01 ou case non voisine de la pièce de J. R. 01) ;
- placer sa troisième pièce (quatre façons) ;
- déplacer une pièce.
Puisqu’il y a 8 possibilités et 8 seulement, il est possible de les coder, en système binaire, à l’aide de 3 informations binaires
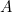 ,
, 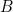 ,
, 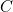 .
.
Nous avons choisi, par convention, le code suivant (tout autre code est valable ; amusez-vous à changer de code alors ce qui suit sera changé et… vous aurez un autre programme pour le même jeu… ). -
![Rendered by QuickLaTeX.com $\begin{specifications}% [label={}] \item{-- pièce 1 (de l'adversaire de J.R.01) :} 001 \item{-- pièce 2 (de l'adversaire de J:R.01) : \\ en case voisine de la pièce de J.R.01} 110 \item {\qquad en case éloignée de la pièce de J.R.01} 010 \item {-- pièce 3 (de l'adversaire de J.R. 01) :\\ en case voisine de la 2e pièce de J.R.01} 101 \item {\qquad en case éloignée de la 2e pièce de J.R.01} 011 \item {\qquad les trois pièces du même côté\\ d'un axe de symétrie de la plaque carrée} 100 \item {\qquad trio (les 3 pièces alignées) :} 111 \item {-- déplacement d'une pièce}: 000 \end{specifications}$](https://jr01.dhenin.fr/wp-content/ql-cache/quicklatex.com-101058e37622e5df1e55899fe823ed52_l3.png)
Quel doit être alors le jeu de l’ordinateur J.R. 01 ?
Nous devons étudier tous les cas. Pour faciliter cette étude nous allons utiliser des figures (1 à 3-d ci-dessous) et le code suivant : numéros 1, 2, 3 pour les pièces de l’adversaire de J.R.01, ces pièces étant représentées par un ▲ ; numéros 1′, 2′,3′ pour celles de J.R.01, ces pièces étant représentées par un ●.
On obtient ainsi pour le J.R.01 qui doit chercher à « coincer » son adversaire :- Au premier coup, la disposition fig. 1.
- Au deuxième coup, la disposition 2-a ou une autre, par exemple 2-b.
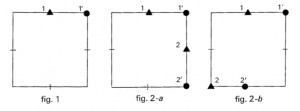
- Au troisième coup, les quatre possibilités sont représentées sur les figures 3-a, 3-b, 3-c, 3-d.
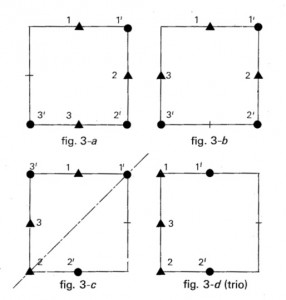 Dans le cas 3-d, l’adversaire enlèvera une plece du J.R. 01. La réponse de celui-ci devra être de « remplacer la pièce enlevée » et l’adversaire sera coincé… et battu.Dans le cas 3-a, on montre que le jeu n’a pas de gagnant !Quoi qu’il en soit, le \textbf{jeu} du J.R.01 comporte quatre possibilités :
Dans le cas 3-d, l’adversaire enlèvera une plece du J.R. 01. La réponse de celui-ci devra être de « remplacer la pièce enlevée » et l’adversaire sera coincé… et battu.Dans le cas 3-a, on montre que le jeu n’a pas de gagnant !Quoi qu’il en soit, le \textbf{jeu} du J.R.01 comporte quatre possibilités : - se placer en case voisine de la dernière pièce posée par l’adversaire ;
- se placer en case voisine de telle sorte que les 4 pièces considérées (1-1′ – 2-2′ ou 2-2′ – 3-3′) forment un parallélogramme (fig. 2-b ou 3-b ou 3-c) ;
- remplacer la pièce enlevée ;
- poursuivre la pièce déplacée par l’adversaire.Pour traduire ces 4 possibilités, il est commode d’avoir 4 sorties : on utilisera alors les lampes
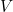 ,
,  ,
, 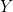 ,
, 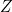 . Chaque possibilité va être codée, par convention, de la façon suivante :
. Chaque possibilité va être codée, par convention, de la façon suivante :

On obtient alors la table de valeur ci-dessous.
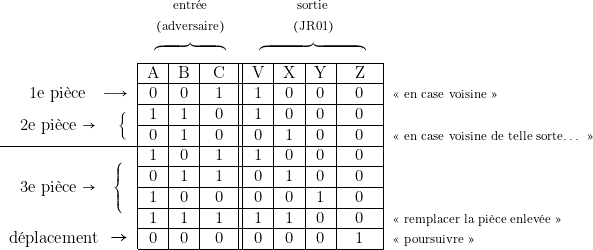
- 3° Expressions algébriques.
Vous savez écrire immédiatement que
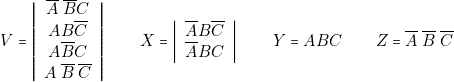
- 4° Simplifications.
- — En regroupant les 1er et 3e termes d’une part, 2e et 4e d’autre part
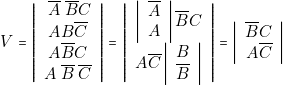 ;
; - — Pour
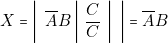 ;
;
- — Pour
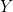 et
et 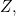 il n’y a pas de simplifications possibles.
il n’y a pas de simplifications possibles.
- — En regroupant les 1er et 3e termes d’une part, 2e et 4e d’autre part
- 5° Schéma du programme.
Dessinez-le. Vous obtiendrez celui de la notice
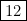
- 6° Un jeu… déduit de ce jeu !
Puisque le jeu du J.R.01 n’a que 4 possibilités, deux sorties suffisent ! Soit
 et
et 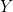 ces sorties.
ces sorties.
Codez, à votre convenance, 00, 01 , 10, 11, les quatre possibilités indiquées. Dressez la nouvelle table de valeurs. Écrivez les nouvelles expressions algébriques. Indiquez le nouveau programme obtenu. Réalisez-le… et comparez…
Jouez 
|
