Notice 11Commande automatique |
- 1° Analyse du problèmeAucune difficulté. C’est un simple problème à trois informations binaires (phénomènes binaires, propositions… ). On va poser, par convention :
@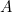 : sens de parcours de l’ascenseur avant l’appel ;
: sens de parcours de l’ascenseur avant l’appel ; 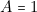 l’ascenseur se dirigeait vers le haut ;
l’ascenseur se dirigeait vers le haut ; 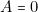 , il se dirigeait vers le bas.
, il se dirigeait vers le bas.
@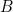 : appel vers le haut ; c’est vrai
: appel vers le haut ; c’est vrai 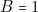 ; ce n’est pas vrai (c’est-à-dire : il n’y a pas appel vers le haut)
; ce n’est pas vrai (c’est-à-dire : il n’y a pas appel vers le haut) 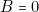 .
.
@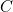 : appel vers le bas ; mêmes conventions pour
: appel vers le bas ; mêmes conventions pour 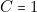 et
et 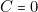 .
.
@À la sortie, c’est-à-dire les manœuvres à exécuter par l’ascenseur sur ordre du J.R. 01, on pose, par convention, que : : commande la porte de l’ascenseur ;
: commande la porte de l’ascenseur ;
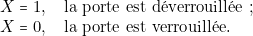
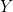 : commande la mise en route du moteur ;
: commande la mise en route du moteur ;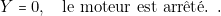
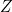 : commande le sens de parcours de l’ascenseur après l’appel ;
: commande le sens de parcours de l’ascenseur après l’appel ;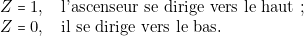
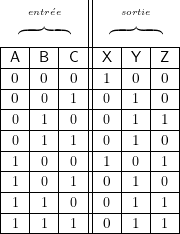
En étudiant chaque cas,on construit aisément la table de valeurs ci-dessous. Faites cette étude… !
- 2° Table de valeurs.
-
Traitons un seul exemple (la dernière ligne) : 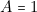 et
et 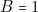 et
et 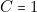 , c’est-à-dire l’ascenseur monte et il reçoit deux appels simultanés du haut et du bas. Que doit-il faire ?
, c’est-à-dire l’ascenseur monte et il reçoit deux appels simultanés du haut et du bas. Que doit-il faire ?
- — La porte doit rester verrouillée :
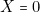 ;
; - — Le moteur doit fonctionner :
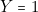
- — L’ascenseur doit poursuivre son ascension :
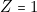
Traitez, de même, les 7 autres cas…
- — La porte doit rester verrouillée :
- 3° Expressions algébriques.
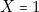 sur les lignes 4 ou 8 c’est-à-dire si :
sur les lignes 4 ou 8 c’est-à-dire si :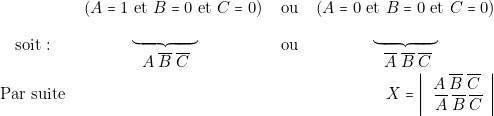
- — De même
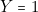 sur les lignes 2 ou3 ou4 ou 6 ou 7 ou 8.
sur les lignes 2 ou3 ou4 ou 6 ou 7 ou 8.
Vous obtenez alors :
![Rendered by QuickLaTeX.com \[ Y=\left|\begin{array}{c} \overline{A}\;\overline{B}C\\ \overline{A}B\overline{C}\\ \overline{A}BC\\ A\overline{B}C\\ AB\overline{C}\\ ABC \end{array}\right| \]](https://jr01.dhenin.fr/wp-content/ql-cache/quicklatex.com-61b4d7f32e5dc2f4c137df4322ac2f15_l3.png)
- — De même
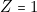 sur les lignes 3 ou 5 ou 7 ou 8.Vous obtenez alors :
sur les lignes 3 ou 5 ou 7 ou 8.Vous obtenez alors :
![Rendered by QuickLaTeX.com \[ Z=\left|\begin{array}{c} \overline{A}B\overline{C}\\ A\;\overline{B}\;\overline{C}\\ AB\overline{C}\\ ABC \end{array}\right| \]](https://jr01.dhenin.fr/wp-content/ql-cache/quicklatex.com-427f3133916523ac0ed0f1cc2165aff1_l3.png)
- — De même
- 4° Simplifications (voir 1re partie, paragraphes 6 et 8).
![Rendered by QuickLaTeX.com \[ X=\left|\begin{array}{c} A\;\overline{B}\;\overline{C}\\ \;\overline{A}\;\overline{B}\;\overline{C} \end{array}\right|=\;\overline{B}\;\overline{C}\mathrm{;} \qquad Y=\left|\begin{array}{c} \;\overline{A}\;\overline{B}C\\ \overline{A}B\overline{C}\\ \overline{A}BC\\ A\overline{B}C\\ AB\overline{C}\\ ABC \end{array}\right| = \left|\begin{array}{c} A\left|\begin{array}{c} B\\ C\\ \end{array}\right|\\ \overline{A}\left|\begin{array}{c} B\\ C \\ \end{array}\right| \end{array}\right|=\left|\begin{array}{c} B\\ C\\ \end{array}\right| \;\mathrm{;} \]](https://jr01.dhenin.fr/wp-content/ql-cache/quicklatex.com-b38490d6858518688ce09d5cfc8a98d6_l3.png)
![Rendered by QuickLaTeX.com \[ Z=\left|\begin{array}{c} \overline{A}B\overline{C}\\ A\;\overline{B}\;\overline{C}\\ AB\overline{C}\\ ABC \end{array}\right| = \left|\begin{array}{c} AB\left|\begin{array}{c} \overline{C}\\ C \end{array}\right|\\ \mathrm{?} \end{array}\right|=\left|\begin{array}{c} AB\\ A\overline{C}\\ B\overline{C} \end{array}\right| \]](https://jr01.dhenin.fr/wp-content/ql-cache/quicklatex.com-049766893cae4b4096eb9341f9c77fee_l3.png)
- 5° Schéma du programme.
Dessinez-le seul. Vous devez retrouver celui indiqué notice
 ou un schéma équivalent.
ou un schéma équivalent.
Jouez 
|
