Notice 6Le jeu des trois verres |
- 1° Analyse du problème.
Soit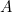 ,
, 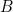 ,
, 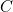 les trois verres. Écrivons 1 si un verre se trouve dansla position « debout », écrivons 0 si un verre se trouve dans la position« renversée ».
les trois verres. Écrivons 1 si un verre se trouve dansla position « debout », écrivons 0 si un verre se trouve dans la position« renversée ».
Les 8 possibilités (cas de 3 propositions) se réduisent immédiatement à… 4 (en « échangeant » le « nom » des verres). À savoir :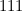 (les 3 verres sont « debout ») ;
(les 3 verres sont « debout ») ; 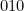 (un verre, celui du milieu,
si l’on veut, est « debout », les 2 autres renversés) ;
(un verre, celui du milieu,
si l’on veut, est « debout », les 2 autres renversés) ; 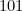 (deux verres « debout», un « renversé », celui du milieu ;
(deux verres « debout», un « renversé », celui du milieu ; 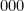 (les trois verres sont « renversés ». Puisque nous avons droit à 3 manipulations
de deux verres chaque fois, cela signifie que nous avons droit à 6changements de
(les trois verres sont « renversés ». Puisque nous avons droit à 3 manipulations
de deux verres chaque fois, cela signifie que nous avons droit à 6changements de 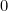 en
en  ou de
ou de  en
en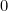 .
.
Par suite les cas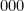 et
et 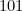 ne peuvent avoir de solution. En trois manipulations on ne peut obtenir que…
ne peuvent avoir de solution. En trois manipulations on ne peut obtenir que… 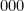 si l’on veut. Les cas
si l’on veut. Les cas 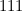 et
et 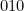 ont une solution.
ont une solution. Laquelle ?
- → Pour
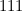 , on passe d’abord à
, on passe d’abord à 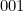 , puis à
, puis à 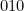 , puis à
, puis à 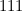 .
.
- → Pour
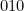 , on passe d’abord à
, on passe d’abord à 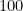 , puis à
, puis à 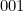 , puis à
, puis à 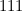 .
.
- → Pour
- 2° Table de valeurs.
Établissons-la pour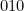 . On obtient (d’après ce qui précède) :
. On obtient (d’après ce qui précède) : 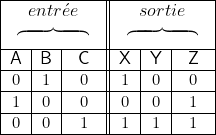
- 3° Expressions algébriques.
- — La lampe
 doit s’allumer si
doit s’allumer si 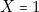 c’est-à-dire sur les lignes
1 ou 3. Or la ligne 1 correspond à (
c’est-à-dire sur les lignes
1 ou 3. Or la ligne 1 correspond à (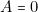 \textbf{et}
\textbf{et} 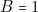 et
et 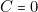 ) soit
) soit 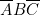 et la ligne
3 correspond à (
et la ligne
3 correspond à (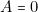 \textbf{et}
\textbf{et} 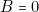 \textbf{et}
\textbf{et} 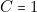 ) soit
) soit
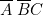 .
.
Donc :
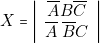
- — La lampe
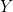 doit s’allumer si
doit s’allumer si 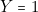 , c’est-à-dire sur la ligne
3. On vient de voir que cette ligne correspond à
, c’est-à-dire sur la ligne
3. On vient de voir que cette ligne correspond à 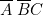 .
.
Donc :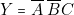 .
.
- — La lampe
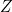 doit s’allumer si
doit s’allumer si 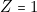 , c’est-à-dire sur les lignes
2 ou 3.
, c’est-à-dire sur les lignes
2 ou 3.
La ligne 2 correspond à (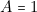 et
et 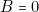 et
et 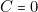 ), soit
), soit 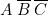
La ligne 3 correspond à (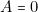 et
et 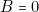 et
et 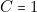 ), soit à
), soit à 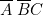
Donc :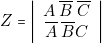
- — La lampe
- 4° Simplifications.
Il n’y en a pas. - 4° Schéma de programme.
- — Pour « alimenter » la lampe
 , il faut deux « colonnes de programmation ». Nous avons choisi les colonnes 2 et 3. Sur la colonne 2, on a réalisé
, il faut deux « colonnes de programmation ». Nous avons choisi les colonnes 2 et 3. Sur la colonne 2, on a réalisé 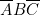 . Sur la colonne 3,
. Sur la colonne 3, 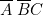 .
D’où
.
D’où 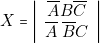
- — Pour
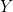 , une seule colonne suffit. Nous avons choisi la colonne
4 sur laquelle on a écrit
, une seule colonne suffit. Nous avons choisi la colonne
4 sur laquelle on a écrit 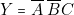 .
.
- — Pour
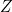 , il faut deux branchements en parallèles. On choisit les
« colonnes de programmation » 5 et 6. Sur 5 on a réalisé
, il faut deux branchements en parallèles. On choisit les
« colonnes de programmation » 5 et 6. Sur 5 on a réalisé 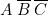 et sur 6,
et sur 6, 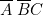 . Donc on a bien
. Donc on a bien 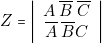
- — Ceci justifie le programme donné dans la notice
 .
.
- — Pour « alimenter » la lampe
Jouez 
|
