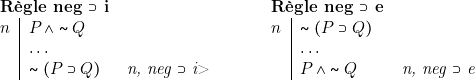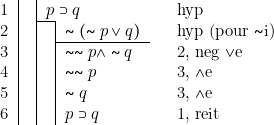La négation |
Jusqu’ici, nous avons admis que, dans les applications, nous traiterions comme atomiques aussi bien les propositions affirmatives que les propositions négatives. Il est toutefois clair que toute proposition négative, disons ![]() , peut se comprendre comme la négation d’une proposition affirmative : non–
, peut se comprendre comme la négation d’une proposition affirmative : non–![]() .
.
Exemples
[1] « 6 n’est pas un nombre premier », soit ![]() peut se comprendre comme :
peut se comprendre comme :
« non : 6 est un nombre premier », soit non-–![]() .
.
[2] « Il n’y a pas de roses sans épines » peut se comprendre comme :
« non : il y a des roses sans épines ».
Le mot « non » joue encore le rôle d’un foncteur propositionnel, mais c’est un foncteur unaire, en ce sens qu’il s’applique à une seule proposition. Il désigne l’opération qui transforme une proposition ![]() en sa négation non
en sa négation non![]() . Nous noterons
. Nous noterons ![]() , ce que d’autres écrivent aussi
, ce que d’autres écrivent aussi ![]() ou
ou ![]() ou
ou ![]() .
.
Il est facile de voir que la négation joue un rôle privilégié en logique. On peut tout d’abord s’assurer sur soi-même qu’il n’est pas immédiat que la négation de « il est bête et méchant » soit « il n’est pas bête ou il n’est pas méchant ». On peut aussi constater que des logiques, comme la logique intuitionniste ou la logique minimale, diffèrent avant tout de la logique classique par l’usage qu’elles font de la négation. Ceci suffit déjà à expliquer pourquoi nous allons procéder en plusieurs étapes et examiner chaque fois la portée des règles introduites.
Règle ![]() i
i
Commençons par poser que, si une proposition ![]() , prise comme hypothèse, conduit à une contradiction — c’est-à-dire qu’il est possible d’en déduire une proposition
, prise comme hypothèse, conduit à une contradiction — c’est-à-dire qu’il est possible d’en déduire une proposition ![]() et la négation de
et la négation de ![]() — alors c’est
— alors c’est ![]() qu’il faut affirmer. Cela nous donne :
qu’il faut affirmer. Cela nous donne :
Règle ![]() i
i
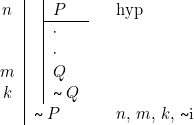
Remarques
|
1) Il s’agit ici d’une règle qui codifie, dans notre système, le raisonnement par l’absurde : toute proposition qui conduit à une contradiction doit être niée. 2) Cette règle est très proche de la règle 3) Cette règle se propose d’introduire un signe « Il est clair que le « |
Exemples
[1] ![]()

[2] ![]()

Remarques
|
1) Il faut se garder de conclure que, puisque l’hypothèse 2) L’exemple [2] permet d’écrire le métathéorème : 3) Rien n’empêche aussi de s’en tenir (avec |
Règle neg ![]() i
i
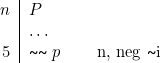
[3] ![]()

Remarques
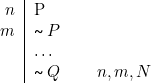
2. On entend volontiers dire qu’« une contradiction conduit à n’importe quoi ». Ce que nous pouvons toutefois établir pour l’instant, c’est que : |
Dérivons maintenant directement trois nouvelles règles :
Règle neg ![]() i (pour introduire une conjonction précédée d’une négation)
i (pour introduire une conjonction précédée d’une négation)

Règle neg ![]() i (pour introduire une disjonction précédée d’une négation)
i (pour introduire une disjonction précédée d’une négation)

Règle neg ![]() e (pour éliminer une disjonction précédée d’une négation)
e (pour éliminer une disjonction précédée d’une négation)

Faisons maintenant le point de la situation. Si nous ajoutons aux règles générales et aux règles pour les fondeurs ![]() ,
, ![]() , et
, et ![]() , la règle
, la règle ![]() i, nous pouvons dériver les règles suivantes :
i, nous pouvons dériver les règles suivantes :
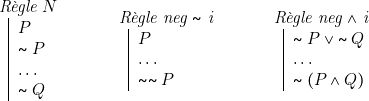
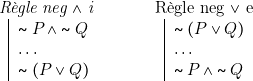
Les deux règles neg ![]() i et neg
i et neg ![]() e constituent l’une des lois de Morgan. Il est tentant de se demander si l’on ne pourrait pas encore dériver la règle neg Ae (avec neg A j, nous obtiendrions l’autre loi de Morgan) et la règle neg
e constituent l’une des lois de Morgan. Il est tentant de se demander si l’on ne pourrait pas encore dériver la règle neg Ae (avec neg A j, nous obtiendrions l’autre loi de Morgan) et la règle neg ![]() e (avec neg
e (avec neg ![]() i nous aurions la loi de double négation). En fait on peut montrer, par des considérations métathéoriques que nous ne rapporterons pas, que la chose n’est pas possible. Cela signifie que nous ne disposons, pour le moment, que d’une forme faible de la négation. On l’appelle parfois la réfutabilité et la logique obtenue équivaut à la logique dite minimale de Johansson (1936). (On trouvera des compléments d’information dans le Fascicule 3).
i nous aurions la loi de double négation). En fait on peut montrer, par des considérations métathéoriques que nous ne rapporterons pas, que la chose n’est pas possible. Cela signifie que nous ne disposons, pour le moment, que d’une forme faible de la négation. On l’appelle parfois la réfutabilité et la logique obtenue équivaut à la logique dite minimale de Johansson (1936). (On trouvera des compléments d’information dans le Fascicule 3).
Comme la limitation fondamentale réside en ce que la règle N ne nous permet que d’arriver à une proposition négative ![]() , nous allons renforcer notre négation en introduisant l’équivalent du principe fameux : ex falso quodlibet sequitur. Nous poserons donc la nouvelle règle suivante :
, nous allons renforcer notre négation en introduisant l’équivalent du principe fameux : ex falso quodlibet sequitur. Nous poserons donc la nouvelle règle suivante :
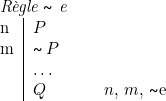
Remarques
|
1. Il est évidemment un peu abusif de considérer cette règle comme une règle d’élimination. La proposition 2. Cette règle dispense de la règle 3. Cette nouvelle règle est cependant plus forte que la règle N, ce qui signifie qu’elle permet de démontrer de nouveaux théorèmes. Exemple
On voit que, si l’on pouvait passer de |
Il s’ensuit que nous disposons maintenant d’un nouveau type de négation, plus fort que la réfutabilité mais pas encore « complet » au sens classique. Cette négation se nomme volontiers l’absurdité et le système obtenu en ajoutant aux règles de la logique minimale la règle ![]() e équivaut à la logique intuitionniste de Heyting (1930).
e équivaut à la logique intuitionniste de Heyting (1930).
Pour terminer, donnons-nous la règle neg ![]() e :
e :
Règle neg ![]() e
e
Nous venons d’esquisser la preuve qu’il est maintenant possible de démontrer ![]() ce qui permet d’affirmer que
ce qui permet d’affirmer que ![]() est équivalent à
est équivalent à ![]() . Il est aussi facile de déduire la règle neg
. Il est aussi facile de déduire la règle neg ![]() e qui manquait :
e qui manquait :
Règle neg ![]() e
e
En effet :
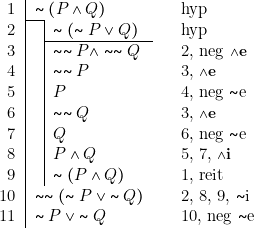
Le système engendré par les règles suivantes : règles générales, règles pour ![]() ,
, ![]() ,
, ![]() , règles
, règles ![]() i,
i, ![]() e et neg
e et neg ![]() e conduit à la {\it logique classique des propositions}. Le métathéorème suivant, dit \emph{principe du tiers exclu}, en est caractéristique :
e conduit à la {\it logique classique des propositions}. Le métathéorème suivant, dit \emph{principe du tiers exclu}, en est caractéristique :
![]()
Preuve
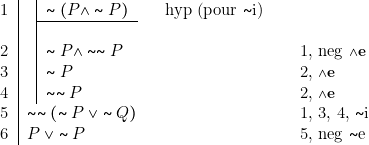
Remarques
1. Ainsi qu’on peut le constater, la ligne 5 s’obtient à l’aide de règles qui sont déjà disponibles en logique minimale. C’est donc bien l’élimination de la double négation qui est caractéristique de la logique classique.
2) Glivenko (1929), comparant la logique intuitionniste I et la logique classique C, a pu établir l’épithéorème suivant :
Si 
|
4. Le lecteur vérifiera qu’en logique classique il est possible de dériver les deux règles suivantes, qui sont très commodes à l’usage :