Les tautologies |
Les tables précédentes permettent d’évaluer n’importe quelle proposition moléculaire ![]() dont les atomes sont composés par les opérateurs
dont les atomes sont composés par les opérateurs ![]() ,
, ![]() ,
, ![]() ,
,![]() ,
, ![]() et
et ![]() que nous venons de définir. Si
que nous venons de définir. Si ![]() contient deux atomes, il y aura
contient deux atomes, il y aura ![]() éventualités à examiner.
éventualités à examiner.
Exemple
![]() =
=![]()
![]()
On a, en disposant les calculs en ligne :
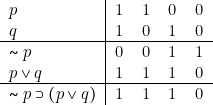
Si ![]() contient trois atomes, on aura
contient trois atomes, on aura ![]() éventualités à étudier, ce que nous ferons en adoptant l’ordre canonique qui figure dans l’exemple suivant :
éventualités à étudier, ce que nous ferons en adoptant l’ordre canonique qui figure dans l’exemple suivant :
Exemple
![]()

D’une façon générale, si ![]() contient les
contient les ![]() atomes
atomes ![]() ,
, ![]() ,
, ![]() ,
, ![]() , il faudra envisager
, il faudra envisager ![]() éventualités. Nous adopterons l’ordre canonique suivant. Les atomes étant ordonnés une fois pour toutes (pratiquement, on choisit l’ordre alphabétique), on écrit les suites :
éventualités. Nous adopterons l’ordre canonique suivant. Les atomes étant ordonnés une fois pour toutes (pratiquement, on choisit l’ordre alphabétique), on écrit les suites :
![]() valeurs 1, suivies de
valeurs 1, suivies de ![]() valeurs 0 ;
valeurs 0 ;
![]() valeurs 1, suivies de
valeurs 1, suivies de ![]() valeurs 0, suivies de
valeurs 0, suivies de ![]() valeurs 1, suivies de
valeurs 1, suivies de ![]() valeurs 0 ;
valeurs 0 ;
![]() valeurs 1, suivies de
valeurs 1, suivies de ![]() valeurs 0, etc.
valeurs 0, etc.
![]() une suite alternée d e1 et de 0.
une suite alternée d e1 et de 0.
Les calculs deviennent assez rapidement fastidieux, mais ils n’offrent jamais de difficultés de principe et, à toute proposition composée de ![]() atomes, on sait faire correspondre une suite ordonnée de
atomes, on sait faire correspondre une suite ordonnée de![]() valeurs 1 et 0.
valeurs 1 et 0.
Exemples

Remarque
L’introduction d’un ordre canonique permet de donner l’évaluation d’une proposition ![]() sans préciser chaque fois à quelles valeurs des atomes correspondent les 1 et les 0 de
sans préciser chaque fois à quelles valeurs des atomes correspondent les 1 et les 0 de ![]() . Ainsi, pour
. Ainsi, pour![]() par exemple, on peut se contenter de donner le quadruple (1 0 0 0).
par exemple, on peut se contenter de donner le quadruple (1 0 0 0).
Répartissons les évaluations en trois catégories, selon (1) qu’il y figure des 1 et des 0 (2) qu’il n’y figure que des 1 et (3) qu’il
n’y figure que des 0. Il existe des propositions qui correspondent à chacune de ces catégories. Toutes celles que nous venons de voir sont des exemples de la première. Comme le montrent les calculs suivants ![]() ,
, ![]() sont des exemples de la deuxième et
sont des exemples de la deuxième et ![]() ,
, ![]() des exemples de la troisième.
des exemples de la troisième.
Calculs
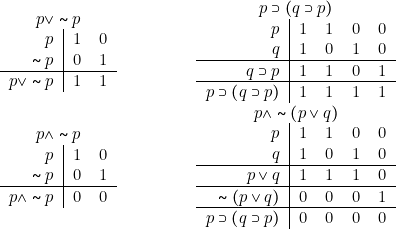
Toute proposition dont l’évaluation ne contient que des 1 est une tautologie et toute proposition dont l’évaluation ne contient que des 0 est une contradiction. Il est clair que si ![]() est une tautologie,
est une tautologie, ![]() sera une contradiction et réciproquement. D’autre part, puisque une proposition atomique
sera une contradiction et réciproquement. D’autre part, puisque une proposition atomique ![]() prend soit la valeur 1 soit la valeur 0, seules des propositions moléculaires peuvent être des tautologies ou des contradictions. Si
prend soit la valeur 1 soit la valeur 0, seules des propositions moléculaires peuvent être des tautologies ou des contradictions. Si ![]() est une tautologie, nous écrirons
est une tautologie, nous écrirons ![]() .
.
Remarques
1. Affirmer, comme nous venons de le faire, qu’une proposition atomique, ne peut être ni une tautologie, ni une contradiction, c’est s’appuyer sur une décision propre au système logique construit et non pas constater un fait d’expérience. La proposition « les célibataires sont des gens mariés » est atomique, en ce sens qu’elle ne contient aucun des opérateurs précédents et elle exprime cependant une contradiction. Toutefois, on sait que, analysée dans la logique des prédicats, elle s’écrira :
![]() où
où ![]() =df
=df ![]() est marié et où être célibataire =df être non marié.
est marié et où être célibataire =df être non marié.
Cette divergence repose sur le fait que « être une expression atomique » n’a pas le même sens dans la logique des propositions et dans celle des prédicats.
2. Nous avons utilisé le même signe ![]() pour dire qu’une proposition était une tautologie et pour dire qu’elle était un théorème (I, p. 21). Il est possible, en prenant des exemples, de s’assurer que si
pour dire qu’une proposition était une tautologie et pour dire qu’elle était un théorème (I, p. 21). Il est possible, en prenant des exemples, de s’assurer que si ![]() est un théorème alors
est un théorème alors ![]() est une tautologie et réciproquement. Toutefois la pratique qui consiste à écrire dans les deux cas
est une tautologie et réciproquement. Toutefois la pratique qui consiste à écrire dans les deux cas ![]() exigerait la démonstration d’un épi-théorème. Une telle démonstration, si elle se voulait rigoureuse, sortirait du propos de cet ouvrage, mais nous y reviendrons cependant en 1.7.
exigerait la démonstration d’un épi-théorème. Une telle démonstration, si elle se voulait rigoureuse, sortirait du propos de cet ouvrage, mais nous y reviendrons cependant en 1.7.
3. Puisqu’une tautologie est vraie, quelles que soient les valeurs de ses atomes, on peut de nouveau dire qu’elle est « vraie dans tous les mondes possibles ». Elle ne fournit ainsi aucune information sur le monde lui-même.
Exemple
« Il y a des hommes sur la planète Mars ou il n’y a pas d’hommes sur la planète Mars », soit ![]() , ne nous renseigne absolument pas sur la planète en question.
, ne nous renseigne absolument pas sur la planète en question.
On dit volontiers pour cela que les tautologies sont vides de sens. En fait, elles expriment des lois logiques en explicitant la façon dont les opérateurs ont utilisés.
Il est de nouveau possible de définir les relations d’implication et d’équivalence entre propositions. Nous poserons encore:
![]()
La relation d’équivalence permet d’énoncer les principales propriétés des opérateurs que nous avons introduits jusqu’ici. Pour les vérifier, il suffit de remplacer toute expression de la forme ![]() par
par ![]() et de s’assurer par le calcul que cette dernière proposition est bien une tautologie. Nous avons :
et de s’assurer par le calcul que cette dernière proposition est bien une tautologie. Nous avons :
(0) ![]() , {\em principe de la double négation};
, {\em principe de la double négation};
(1) les opérations ![]() ,
, ![]() ,
, ![]() et
et ![]() {\em sont commutatives} :
{\em sont commutatives} :![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
(2) Elles sont {\em associatives}
![]() ,
, ![]()
![]() ,
, ![]() ;
;
3. Les opérations ![]() et
et ![]() sont {\em idempotentes} :
sont {\em idempotentes} :
![]() ,
, ![]() ;
;
4. Les opérations ![]() et
et ![]() sont {\em distributives} l’une par rapport à l’autre :\\
sont {\em distributives} l’une par rapport à l’autre :\\
![]() \\
\\
![]()
L’opération ![]() ne jouit d’aucune des trois premières propriétés et l’opération~
ne jouit d’aucune des trois premières propriétés et l’opération~![]() n’est pas idempotente~:
n’est pas idempotente~: ![]() est une tautologie.
est une tautologie.
Remarque
Une expression comme ![]() n’est pas homogène. En signes
n’est pas homogène. En signes ![]() ,
, ![]() et
et ![]() font partie du système que nous étudions. Mais le
font partie du système que nous étudions. Mais le ![]() est une abréviation de la langue de communication. Il sert à dire : « est équivalente à ». Ce fait nous a permis d’économiser les parenthèses où, pour éviter des confusions, il faudrait écrire
est une abréviation de la langue de communication. Il sert à dire : « est équivalente à ». Ce fait nous a permis d’économiser les parenthèses où, pour éviter des confusions, il faudrait écrire ![]() puisque
puisque ![]() est aussi un signe du calcul, nous avons pu nous contenter d’écrire
est aussi un signe du calcul, nous avons pu nous contenter d’écrire ![]() . Nous utiliserons systématiquement cette pratique dans ce qui suit.
. Nous utiliserons systématiquement cette pratique dans ce qui suit.
La relation d’équivalence permet aussi de montrer que les opérateurs définis par les tables qui précèdent ne sont pas indépendants les uns des autres. Ainsi on aura :
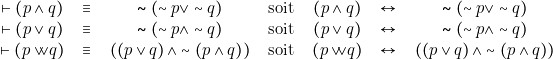
Les deux premières équivalences correspondent aux lois de Morgan (I. p38). Assurons-nous de la troisième~: \label{De_Morgan}
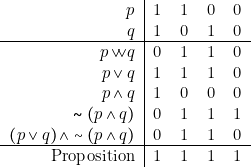
On aura encore : ![]() \\ et
\\ et ![]() .
.
Introduisons enfin un nouvel opérateur ![]() tel que
tel que ![]() s’interprète comme « pas à la fois
s’interprète comme « pas à la fois ![]() et
et ![]() ».
».
Cela conduit à poser la table :
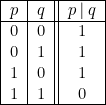
Il est facile de s’assurer que l’on a alors les équivalences suivantes :
![]() \qquad{}
\qquad{}![]() \qquad{}
\qquad{}![]() .
.
Remarque
L’opérateur ![]() dont l’évaluation est (0 0 0 1) conduit aux équivalences :
dont l’évaluation est (0 0 0 1) conduit aux équivalences :
![]() \qquad{}
\qquad{}![]() \qquad{}
\qquad{}![]() .
.
On voit ainsi qu’un seul opérateur, soit ![]() , soit
, soit ![]() , permet de définir tous les autres par des équivalences.
, permet de définir tous les autres par des équivalences.
Bien que représentant des lois logiques, les tautologies ne permettent pas d’effectuer des déductions. Toutefois, si une déduction est effectuée, elles permettent de s’assurer de sa correction.
Exemple
« Ceux qui veulent la paix préparent la guerre. Vous ne préparez pas la guerre, donc vous ne voulez pas la paix ».
Nous poserons :
![]()
Le raisonnement part des deux prémisses ![]() et
et ![]() et il conclut
et il conclut ![]() . Il suffit de voir si la conjonction des prémisses implique la conclusion, donc si
. Il suffit de voir si la conjonction des prémisses implique la conclusion, donc si ![]() ou encore si
ou encore si ![]() .
.
C’est bien le cas, ce qui montre tout à la fois que le raisonnement est correct et qu’il ne suffit pas d’être logique pour faire le bonheur des peuples.
