Le groupe I, N, R, D

1) passer d’une proposition à sa négation
2) remplacer les atomes $\mathbf{p}$ par $\mathbf{\sim\!\!p}$ et réciproquement
3) remplacer $\mathbf{\vee}$ par $\mathbf{\wedge}$ et réciproquement.

Celles-ci ne sont pas sans liens entre elles et c’est même ce que la règle exprime. Toutefois il est intéressant d’étudier la chose d’une façon encore un peu différente. Pour simplifier les écritures, nous nous en tiendrons aux éléments de $\Pi_{2}$ , mais les considérations qui suivent sont tout à fait générales.

Commençons par convenir que les lettres a’, b’, c’, d’ représenteront toujours les valeurs opposées aux lettres a, b, c, d. Donc
si $a=1$ , $a'=0$ , si $a=0$ , $a'=1$ , et de même pour b’, c’, d’. Définissons alors la transforamtion de négation, notée N, et qui fait passer la classe d’équivalence [ a b c d ] à la classe [ a’ b’ c’ d’ ].

N [ a b c d ] = [ a’ b’ c’ d’ ].

Il est clair que N [ a’ b’ c’ d’ ] = [ a b c d ], c’est-à-dire que, si l’on applique deux fois de suite la transformation, on retrouve la classe dont on était parti. Il est commode, pour formuler la chose, d’introduire la transformation identique I, définie de la façon suivante :

I [ a b c d ] = [ a b c d ].

On pourra donc écrire :

NN [ a b c d ] = N [ a’ b’ c’ d’ ] = [ a b c d ] = I [ a b c d ], ou encore :
NN = I . Convenons d’un abus de langage et d’écriture et disons que nos transformations font passer d’une proposition (élément de la classe initiale) à une proposition (élément de la classe finale).

Ainsi nous écrirons par exemple :

N(1000) = (0111) et même N( $p\,\wedge q$ ) = $p\mid q$ .

Mais on voit par le calcul que $p \mid q \Leftrightarrow \sim\!\!p\,\vee \sim\!\!q$ et l’on peut donc écrire :

N $(p\,\wedge q)=\sim\!\!p\,\vee \sim\!\!q$ .

On aura de même :

N ( $1110$ ) = ( $0001$ )

soit encore N ( $p\,\vee q$ ) = $\sim\!\!p\,\wedge \sim\!\!q$ .

Si l’on applique N aux trois autres conjonctions élémentaires et aux trois autres disjonctions élémentaires, on constate que la transformation consiste :

1) à remplacer les atomes $p$ et $q$ par $\sim\!\!p$ et $\sim\!\!q$ et réciproquement,
2) à remplacer les $\wedge$ par $\vee$ et réciproquement.

Remarque

C’est ce qu’exprimaient les règles neg $\wedge$ et neg $\mathbf{\vee}$ (V. I, 1.9).

Définissons maintenant la transformation R de la façon suivante :

R [a b c d ] = [d c b a ].

II est clair que l’on a de nouveau RR = I. En effet :

RR [a b c d ] = R[d c b a ] = [a b c d ] = I [a b c d ].

Nous aurons ainsi, par le même abus que tout à l’heure :

R( $1000$ )=( $0001$ ) ou R $(p\,\wedge q)=\sim\!\!p\,\wedge\sim\!\!q$

R( $1110$ )=( $0111$ ) ou R $(p\,\vee q)=\sim\!\!p\,\vee \sim\!\!q$

Et l’on peut constater que, appliquée à une conjonction élémentaire ou à une disjonction élémentaire, la transformation R, consiste à remplacer les atomes $p$ et $q$ par et $\sim\!\!p$ et $\sim\!\!q$ et réciproquement.

Remarque

Appliquée à une évaluation donnée, R consiste donc à la lire de droite à gauche. Ceci explique que, en décrivant la façon de construire une \textsc{fncc } (V. p. 21) nous ayons dû procéder dans l’ordre\emph{
d, c, b, a}.

Appliquée à la classe [ $1011$ ], R conduit à [ $1101$ ].
Donc, on a en particulier

R $(p \supset q) = q \supset p$ .

C’est la raison pour laquelle nous appellerons R la transformation réciproque.

Définissons enfin, avec ces notations, la transformation duale (V. p. 6), que nous noterons D :

D [a b c d] = [d’c’b’a’]. On a encore DD = I puisque

DD [a b c d] = D [d’c’b’a’] = [a b c d] = I [a b c d].

Et en particulier :

D ( $1000$ ) = ( $1110$ ) ou D $(p\,\wedge q) = p\,\vee q$

D ( $1110$ ) = ( $1000$ ) ouD $(p\,\vee q) = p\,\wedge q$ .

D’une façon générale, appliquée à une conjonction élémentaire ou à une disjonction élémentaire, la transformation D consiste à remplacer les $\wedge$ par $\vee$ et réciproquement.

On constate, pour ainsi dire, que R et D accomplissent chacune une part de ce qu’effectue la transformation N :

1) R agit sur la valeur des atomes
2) D agit sur l’opérateur.

Ceci s’exprime rigoureusement en montrant que RD = DR = N

RD [a b c d] = R [d’ c’ b’ a’] = [a’ b’ c’ d’] = N [a b c d]

DR [a b c d] = D [d c b a] = [a’ b’ c’ d’] = N [a b c d].

Remarques

1) Il arrive assez souvent que dans la pensée spontanée, la transformation R soit utilisée comme négation. Ainsi peut-on observer des dialogues de la forme suivante :

— C’est un journal bête et méchant.
— C’est faux : il n’est ni bête, ni méchant.

La transformation N aurait conduit à : « Il n’est pas bête ou pas méchant ».

— L’étude des transformations ci-dessus a été faite pour la première fois par Jean Piaget qui appelait D la corrélative et la notait en conséquence C (V. la bibliographie à la fin du fascicule).

Il nous reste à montrer que les quatre transformations I, N, R, D forment un système, au sens fort du terme. Posons pour cela, T = df {I, N, R, D}. Calculons l’effet de l’application successive à une classe de deux quelconques des éléments de T, c’est-à-dire calculons toutes les transformations XY, où X et Y sont éléments de T. Le résultat est fourni par la table ci-contre. Les calculs n’offrent aucune difficulté.
Ils se font sur le modèle de RD et DR qui précède.
$\begin{tabular}{c|cccc} & {\bf I} & {\bf N} & {\bf R} & {\bf D} \tabularnewline \hline {\bf I} & {\bf I} & {\bf N} & {\bf R} & {\bf D} \tabularnewline {\bf N} & {\bf N} & {\bf I} & {\bf D} & {\bf R} \tabularnewline {\bf R} & {\bf R} & {\bf D} & {\bf I} & {\bf N} \tabularnewline {\bf D} & {\bf D} & {\bf R} & {\bf N} & {\bf I} \tabularnewline \end{tabular}$

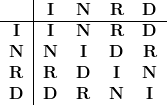
Il est alors possible de faire les cinq remarques suivantes :

1) Si $X,\: Y\in T$ , $XY\in T$ . La composition de deux transformations de $T$ ne fait pas sortir de l’ensemble $T$ .
2) Si $X,\: Y\:,Z\in T$ , $(XY)Z=X(YZ)$ . La composition est associative.

Il est un peu long de s’assurer complètement de la chose, mais la façon de procéder est élémentaire. Faisons-le pour NRD.

3) Calcul de (NR )D :

D [a b c d] = [d’ c’ b’ a’]

NR [d’ c’ b’ a’] = N [a’ b’ c’ d’] = [a b c d] = I [a b c d]

Donc (NR )D = I .

4) Calcul de N(RD) :

RD [a b c d] = R [d’ c’ b’ a’] = [a’ b’ c’ d’]

N [a’ b’ c’ d’] = [a b c d] = I [a b c d].

Donc N (RD ) = I et on a bien (NR )D = N (RD ).

Il existe une transformation identique I.
Si $X\in T$ , il existe $Y\in T$ telle que $XY=YX=$ I .

$Y$ est l’inverses de $X$ et ici chaque transformation est sa propre inverse.

5) $X,\: Y\in T$ , $XY=YX$ . La composition est commutative ce qui se voit sur la table ci-dessus : elle est symétrique par rapport à la diagonale I – I.

Ces cinq faits permettent d’affirmer que l’on a affaire à un groupe abélien et l’on peut montrer qu’il est isomorphe au fameux groupe de Klein (mathématicien allemand : 1849-1925).

Remarque

Il existe naturellement d’autres transformations entre les 16 classes d’équivalence dont certaines forment aussi des groupes (V. Fascicule III).

Les formes normales

Une axiomatisation

JR01

L'ordinateur. Oscar d'or 1970

Toutes directions

Algotaf

Détour de maths

Helpman

Le blog de Mathilde

Philo en terminale

Scilicet

Le site de Sacha

Time protocole (entp)

Archives radio

Le groupe I, N, R, D