Théorèmes, métathéorèmes, règles dérivées

La relation d'implication et celle d'équivalence

 Proposition disjonctive
Page suivante


Partons de la notion de proposition conditionnelle. Une telle proposition peut être vraie ou fausse comme n’importe quelle autre. Ainsi la proposition
« Si X est marié, il a une seule femme légitime » est vraie en Europe, fausse dans certaines civilisations. D’autre part, une proposition peut être vraie pour diverses raisons : juridiques, physiques, logiques, etc.

Considérons alors une proposition conditionnelle qui est vraie pour des raisons logiques. Cela signifie qu’elle est un théorème, donc de la forme \vdash P\supset Q. Tel est, par exemple, le cas de la proposition « p\supset(q\supset p) », si on pose P =df p et Q =df p\supset q. Il est clair que, dans ces conditions, l’antécédent P et le conséquent Q de la conditionnelle ne sont pas quelconques. En d’autres termes, si la proposition conditionnelle P\supset Q est un théorème logique, c’est qu’il existe une certaine relation entre P et Q. Nous dirons alors (et seulement alors) que P implique Q (certains disent : P implique matériellement Q) et nous noterons : P\rightarrow Q. Ceci conduit à poser :

Df\rightarrow : P\rightarrow Q=df \vdash P\supset Q

soit : « P implique Q » veut dire que la proposition conditionnelle « si P alors Q » est un théorème logique.

Remarques

Il est très important de ne pas confondre les signes « \rightarrow » et « \supset ». Le premier est un signe de relation (un relateur), le second est un signe d’opération (un opérateur ou, comme nous disons, un foncteur). L’analogie arithmétique suivante permettra de comprendre pourquoi la confusion est malheureusement facile en logique. Le signe « < » est un relateur en arithmétique. On écrit, par exemple : 3<10. A ceci correspond la proposition « 3 est plus petit que 10 ». Par ailleurs, on écrit aussi en arithmétique : 3+10. Le signe « + » est un opérateur et l’expression ne correspond pas à une proposition, mais elle désigne le nombre 13.
En logique toutefois P\rightarrow Q se traduit par une proposition : « P implique Q » et P\supset Q se traduit aussi par une proposition : « si P alors Q ». Cela n’empêche pas la distinction conceptuelle, mais elle est évidemment moins claire. On pourrait parler, comme le faisait Georges Boole (18151864), d’une proposition primaire pour P\supset Q et d’une proposition secondaire pour P\rightarrow Q. La difficulté tient, en partie, à ce que les langues naturelles ne possèdent pas de moyens systématiques propres à assurer la distinction entre ces deux espèces de propositions.
Donnons à P valeur p et à Q la valeur q\supset p. On a alors \vdash P\supset Q, soit par définition P\rightarrow Q.
Dès lors :

1) P\supset Q, soit « si p alors q\supset p » est une proposition qui appartient à notre système.
2) P\rightarrow Q, soit « p implique q\supset p » est un énoncé qui appartient à la métalangue.
Et l’on voit que nous avons un moyen systématique de distinguer les propositions primaires (du système) des propositions secondaires (qui portent sur le système).

Étudions maintenant quelques unes des propriétés de cette relation d’implication.

1) Elle est réflexive : P\rightarrow P
En effet, par définition, P\rightarrow P signifie \vdash P\supset P, ce qui est le métathéorème (1) du § ? ?

2) Elle est transitive : P\rightarrow Q et Q\rightarrow M\;\Longrightarrow\; P\rightarrow M
Il faut donc montrer que si \vdash P\supset Q et si \vdash Q\supset M, alors on a \vdash P\supset M.

C’est l’exemple d’application que nous avons donné de l’épithéorème 2.

Puisque (c’est une définition reçue en algèbre) toute relation qui est à la fois réflexive et transitive est une relation de préordre, nous pouvons affirmer que l’implication est une \emph{relation de préordre}.

D’une façon analogue, nous allons partir de la proposition biconditionnelle. Elle est de la forme P\equiv Q, soit P ssi Q. Si maintenant les propositions désignées par P et Q sont telles que la proposition désignée par P\equiv Q est un théorème, donc si \vdash P\equiv Q, c’est qu’il existe entre elles une certaine relation que nous noterons \leftrightarrow.

Df\leftrightarrow : P\leftrightarrow Q =df \vdash P\equiv Q.

Étudions aussi cette relation.

1) Elle est réflexive : P\leftrightarrow P Par le métathéorème (4) du § ? ?.
2) Elle est symétrique : P\leftrightarrow Q\Longrightarrow Q\leftrightarrow P

Par le métathéorème (5) du § ? ? et l’exemple d’application de l’épithéorème 1.

3) Elle est transitive : P\leftrightarrow Q et Q\leftrightarrow M\Longrightarrow P\leftrightarrow M

Par le métathéorème (6) du § ? ? et l’épithéorème 1.

Il s’ensuit que, par définition, la relation est une relation d’équivalence.

Les logiciens ont l’habitude de l’appeler simplement la relation d’équivalence. C’est donc un abus de langage, mais il est reçu.

Ceci nous permet de revenir à la relation d’implication. Nous savons déjà qu’il s’agit d’une relation de préordre. Mais elle jouit encore d’une troisième propriété.

3) Elle est antisymétrique : P\rightarrow Q et Q\rightarrow P\Longrightarrow P\leftrightarrow Q

Par le métathéorème (3) du § ? ?.

On convient de dire que la relation d’implication, qui est donc réflexive, transitive et antisymétrique est une relation d’ordre.

Notons enfin que les métathéorèmes (7), (8) et (9) du § ? ? peuvent s’écrire :

\begin{tabular}{lclll} {\small $P\leftrightarrow P\wedge P$} & {\small :} & {\small $P$} & {\small est équivalente à } & {\small $P\leftrightarrow P$}\tabularnewline {\small $P\wedge Q\leftrightarrow Q\wedge P$} & {\small :} & {\small $P\wedge Q$} & {\small est équivalente à} & {\small $Q\wedge P$}\tabularnewline {\small $\left(P\wedge Q\right)\wedge M\leftrightarrow P\wedge\left(Q\wedge M\right)$} & {\small :} & {\small $\left(P\wedge Q\right)\wedge M$} & {\small est équivalente à} & {\small $P\wedge\left(Q\wedge M\right)$}\tabularnewline \end{tabular}

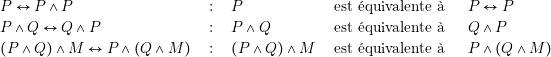
Ces trois équivalences expriment des propriétés importantes du fondeur \wedge, à savoir que l’opération de conjonction est idempotente, commutative et associative.
Remarque

Il faut prendre garde de ne pas confondre les termes : 1) Réflexif, symétrique et transitif, qui désignent des propriétés de certaines relations et 2) Idempotent, commutatif et associatif, qui désignent des propriétés de certaines opérations.

Théorèmes, métathéorèmes, règles dérivées
 		Proposition disjonctive
Page suivante