Les seize opérateurs binaires

Les formes normales

 Le groupe I, N, R, D
Page suivante

Commençons par résoudre le problème suivant. Soit P et Q deux propositions éléments de \Pi_{_{2}}. Nous savons que chacune a pour évaluation l’un des 16 quadruples de la forme (\emph{a b c d}). Comment calculer, à partir d’eux, l’évaluation de P\vee Q ?
Exemple

Nous savons que l’évaluation de p\equiv q est (1001) et que celle de \sim p(q) est (0011).
Il s’agit donc de trouver l’évaluation de (p\equiv q)\vee\sim p(q).
On a les calculs suivants :
\begin{tabular}{r|cccc} $p\equiv q$ & 1 & 0 & 0 & 1\tabularnewline $\sim p(q)$ & 0 & 0 & 1 & 1\tabularnewline \hline \hline $(p\equiv q)\vee\sim p(q)$ & 1 & 0 & 1 & 1\tabularnewline \end{tabular}
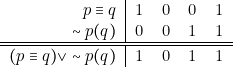
On constate que, si à l’une des places \emph{a, b, c, d} de l’un des quadruples au moins il y a 1, il y aussi 1 dans le quadruple résultant. C’est tout simplement une autre façon de décrire la table de vérité de \vee.
Ceci permet de résoudre le problème inverse. Connaissant l’évaluation d’une proposition M, disons (1011), trouver deux propositions P et Q telles que P\vee Q soit équivalente à M. Un tel problème admet généralement plusieurs solutions.

Exemples
\begin{tabular}{ccc} \begin{tabular}{ccc} $(1001)$ & soit & $p\equiv q$\tabularnewline $(0011)$ & soit & $\sim p(q)$\tabularnewline \hline \hline $(1011)$ & soit & $M$\tabularnewline \end{tabular} & \hspace{1cm} & % \begin{tabular}{ccc} $(0010)$ & soit & $\sim p\wedge q$\tabularnewline $(1011)$ & soit & $p\supset q$\tabularnewline \hline \hline $(1011)$ & soit & $M$\tabularnewline \end{tabular}\tabularnewline & & \tabularnewline \begin{tabular}{ccc} $(1010)$ & soit & $q(p)$\tabularnewline $(1001)$ & soit & $p\equiv q$\tabularnewline \hline \hline $(1011)$ & soit & $M$\tabularnewline \end{tabular} & & \tabularnewline \end{tabular}
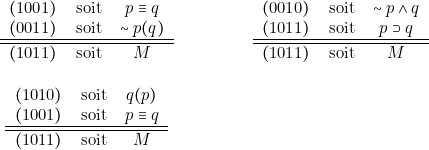
Allons plus loin. On remarquera d’une part que rien n’empêche de chercher une proposition équivalente à M qui contienne plus d’un opérateur \vee et que d’autre part quatre propositions jouissent de la propriété de n’avoir qu’un seul 1 dans leur évaluation. Ce sont p\wedge q soit (1000), p\wedge\sim q soit (0100), \sim p\wedge q soit (0010) et \sim p\wedge\sim q soit (0001).
Nous les appellerons les conjonctions élémentaires. Ces conjonctions élémentaires vont toujours suffire à écrire par disjonction, une proposition équivalente à tout élément de \Pi_{2}, donné.
Exemple
Si nous reprenons M =df p\supset q dont l’évaluation est (1011), on aura :
\left(p\wedge q\right)\vee\left(\sim p\wedge q\right)\vee\left(\sim p\wedge\sim q\right)\leftrightarrow p\supset q.

En effet, la disjonction y est associative et il vient :
\begin{tabular}{r|cccc} $p\wedge q$ & 1 & 0 & 0 & 0\tabularnewline $\sim p\wedge q$ & 0 & 0 & 1 & 0\tabularnewline $\sim p\wedge\sim q$ & 0 & 0 & 0 & 1\tabularnewline \hline \hline $\left(p\wedge q\right)\vee\left(\sim p\wedge q\right)\vee\left(\sim p\wedge\sim q\right)$ & 1 & 0 & 1 & 1\tabularnewline \end{tabular}

D’une façon plus générale, si P est une proposition dont l’évaluation est (a b c d), on obtiendra une proposition qui lui est équivalente, en écrivant la disjonction suivante :

\begin{tabular}{lcccc} $p\wedge q$ & & si $a=1$, & & rien si $a=0$\tabularnewline $p\wedge\sim q$ & & si $b=1$, & & rien si $b=0$\tabularnewline $\sim p\wedge q$ & & si $c=1$, & & rien si $c=0$\tabularnewline $\sim p\wedge\sim q$ & & si $d=1$, & & rien si $d=0$\tabularnewline \end{tabular}

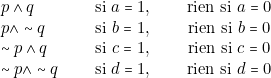
Exemples
\begin{tabular}{ll} $p\equiv q\leftrightarrow\left(p\wedge q\right)\vee\left(\sim p\wedge\sim q\right)$ & Évaluation$(1001)$\tabularnewline $p\vee q\leftrightarrow\left(p\wedge q\right)\vee\left(p\wedge\sim q\right)\vee\left(\sim p\wedge q\right)$ & Évaluation$(1110)$\tabularnewline \end{tabular}

On appelle forme normale disjonctive complète (fndc)
d’une proposition donnée P la disjonction de conjonctions élémentaires qui lui est équivalente.

Remarques

1) La fndc d’une proposition est univoquement déterminée à l’ordre des termes près. On pourra donc parler de la fndc d’une proposition P.

2) La  fndc d’une conjonction élémentaire est cette conjonction elle-même. Il s’agit d’un cas dégénéré de disjonction.

3) Seules les propositions contradictoires de la forme p\bot q n’ont pas de fndc.

4) Les tautologies sont caractérisées par le fait que leur fndc  contient les quatre conjonctions élémentaires.

La définition de la notion de fndc  ne spécifie pas que P contient deux atomes. En effet, quel que soit le nombre des atomes, il sera toujours possible de refaire les raisonnements ci-dessus. La définition est donc générale.

Exemple

Nous allons chercher la fndc de la proposition p\equiv\left(q\wedge m\right). Celle-ci contient les trois atomes p, q et m. Nous aurons donc affaire à 2^{3}=8 conjonctions élémentaires que nous écrirons dans l’ordre canonique.
\begin{tabular}{clcc} (1) & ~~~$p\wedge q\wedge m$ & & soit (10000000)\tabularnewline (2) & ~~~$p\wedge q\wedge\sim m$ & & soit (01000000)\tabularnewline (3) & ~~~$p\wedge\sim q\wedge m$ & & soit (00100000)\tabularnewline (4) & ~~~$p\wedge\sim q\wedge\sim m$ & & soit (00010000)\tabularnewline (5) & $\sim p\wedge q\wedge m$ & & soit (00001000)\tabularnewline (6) & $\sim p\wedge q\wedge\sim m$ & & soit (00000100)\tabularnewline (7) & $\sim p\wedge\sim q\wedge m$ & & soit (00000010)\tabularnewline (8) & $\sim p\wedge\sim q\wedge\sim m$ & & soit (00000001)\tabularnewline \end{tabular}

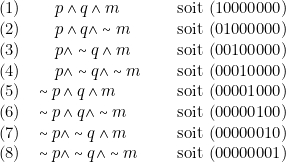
Il suffit maintenant de calculer l’évaluation de p\equiv(q\wedge m) pour être à même d’écrire sa fndc.
\begin{tabular}{l|cccccccc} p & 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0\tabularnewline q & 1 & 1 & 0 & 0 & 1 & 1 & 0 & 0\tabularnewline m & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0\tabularnewline \hline $q\wedge m$ & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0\tabularnewline \hline \hline Proposition & 1 & 0 & 0 & 0 & 0 & 1 & 1 & 1\tabularnewline \end{tabular}

La fndc contiendra donc les conjonctions élémentaires numéros (1), (6), (7) et (8) :

\left(p\wedge q\wedge m\right)\vee\left(\sim p\wedge q\wedge\sim m\right)\vee\left(\sim p\wedge\sim q\wedge m\right)\vee\left(\sim p\wedge\sim q\wedge\sim m\right).

Il existe une seconde forme normale dite conjonctive. Pour le voir, revenons aux éléments de \Pi_{2} et partons des quatre propositions suivantes, que nous appellerons les disjonctions élémentaires :
\begin{tabular}{rlcrl} $p\vee q$ & soit (1110) & \hspace{1cm} & $p\vee\sim q$ & soit (1101)\tabularnewline $\sim p\vee q$ & soit (1011) & & $\sim p\vee\sim q$ & soit (0111)\tabularnewline \end{tabular}

La table de la conjonction \wedge montre qu’il est possible d’obtenir une proposition quelconque d’évaluation (\emph{a b c d}) en écrivant la conjonction suivante :


\begin{tabular}{rcccc} $p\vee q$ & & si $d=0$, & & rien si $d=1$\tabularnewline $p\vee\sim q$ & & si $c=0$, & & rien si $c=1$\tabularnewline $\sim p\vee q$ & & si $b=0$, & & rien si $b=1$\tabularnewline $\sim p\vee\sim q$ & & si $a=0$, & & rien si $a=1$\tabularnewline \end{tabular}

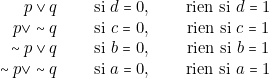
Exemple

Soit P =df p\equiv q, proposition dont l’évaluation est (1001). Il vient \left(p\vee\sim q\right)\wedge\left(\sim p\vee q\right),
proposition équivalente à P. En effet :

\begin{tabular}{r|cccc} $p\vee\sim q$ & 1 & 1 & 0 & 0\tabularnewline $\sim p\vee q$ & 1 & 0 & 1 & 0\tabularnewline \hline \hline $\left(p\vee\sim q\right)\wedge\left(\sim p\vee q\right)$ & 1 & 0 & 0 & 1\tabularnewline \end{tabular}

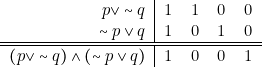
On appelle forme normale conjonctive complète (fncc) d’une proposition P la conjonction de disjonctions élémentaires qui lui est équivalente.

Remarques

1) On notera que la fncc d’une proposition est univoquement déterminée, qu’il existe des conjonctions dégénérées, qu’une contradiction est caractérisée par la présence des quatre disjonctions élémentaires, que les tautologies n’ont pas de\textsc{ fncc} et que la définition ci-dessus est valable pour un nombre quelconque d’atomes.
2) Il existe une relation intéressante entre la fndc d’une proposition et sa fncc. Voyons-le sur un exemple.

Soit P =df p\equiv q proposition dont l’évaluation est (1001). Nous avons vu d’autre part que :

la fndc  de P est (p\wedge q)\vee(\sim p\wedge\sim q)\\
la fncc  de P est \left(p\vee\sim q\right)\wedge\left(\sim p\vee q\right)

Considérons maintenant \sim P. Son évaluation découle de celle de P, par l’application de la transformation de négation. C’est
(0110). Or, la fndc de \sim P est (\sim pA\wedge q)\vee(pA\wedge\sim q). Elle est donc composée des conjonctions élémentaires qui manquent dans la fndc de P. Dès lors, si dans la fndc

de P, on permute les signes \wedge et \vee, on obtient tout justement la fndc de P.

Il en découle la règle de dualité suivante : Soit P une proposition mise en fndc. On obtient la fncc de \sim P en remplaçant chaque atome par sa négation et en échangeant les signes \vee et \wedge. Si P est mise en fncc , on obtiendra la fndc   de P par les mêmes opérations.

Exemple

Soit la proposition p\supset q dont la fndc est (p\wedge q)\vee(\sim p\wedge q)\vee(p\wedge q)\vee(\sim p\wedge\sim q). La fncc de \sim\left(p\supset q\right) sera \left(\sim p\vee\sim q\right)\wedge\left(p\vee\sim q\right)\wedge\left(p\vee q\right).
Les opérateurs \vee et \wedge étant commutatifs, l’ordre est sans importance. De plus nous avons fait tacitement usage du principe
de la double négation.

Vérification

L’évaluation de p\supset q est (1011). Donc celle de \sim(p\supset q) est (0100). Et on a :

\begin{tabular}{c|cccc} $p\wedge q$ & 1 & 0 & 0 & 0\tabularnewline $\sim p\wedge q$ & 0 & 0 & 1 & 0\tabularnewline $\sim p\wedge\sim q$ & 0 & 0 & 0 & 1\tabularnewline \hline \hline Disjonction & 1 & 0 & 1 & 1\tabularnewline \end{tabular}\hspace{1cm} % \begin{tabular}{c|cccc} $\sim p\vee\sim q$ & 0 & 1 & 1 & 1\tabularnewline $p\vee\sim q$ & 1 & 1 & 0 & 1\tabularnewline $p\vee q$ & 1 & 1 & 1 & 0\tabularnewline \hline \hline Conjonction & 0 & 1 & 0 & 0\tabularnewline \end{tabular}

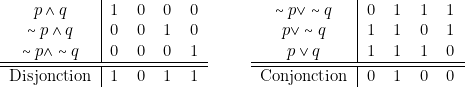
Cette remarquable propriété de dualité explique qu’il y ait eu intérêt à considérer la disjonction non exclusive \vee comme plus fondamentale que la disjonction exclusive \mbox{\ensuremath{\vee}\negthickspace\negthickspace\ensuremath{\vee}} (V. I. p. 29).

S’il est sans grand inconvénient que la fndc d’une contradiction n’existe pas, il peut être très gênant que la fncc d’une tautologie ne puisse s’écrire. Nous allons pour cela introduire une autre espèce de forme normale conjonctive, qui ne sera plus complète et que nous nommerons simplement fnc

Soit une proposition quelconque, disons \sim\left(p\supset q\right)\equiv p. Il est possible de transformer une telle expression par des substitutions d’équivalences que nous avons examinées plus haut. Nous ferons usage :

1) Du fait que \wedge et \vee sont commutatives, associatives et distributives l’une par rapport à l’autre (p. \pageref{associative}
et \pageref{De_Morgan}) ; <————–
2) Que le principe de la double négation est valide (p. \pageref{associative}) ;
3) Que l’on dispose des lois de Morgan (p. \pageref{De_Morgan}) ;
4) Que l’on peut exprimer \supset et \equiv à l’aide de \sim, \vee et \vee (p. \pageref{De_Morgan}).

Appliquons ceci à la proposition donnée. Nous indiquons à côté de chaque ligne à quel groupe d’équivalences il faut faire appel pour passer à la ligne suivante :

\begin{tabular}{clcl} 1. & $\sim\left(p\supset q\right)\equiv p$ & & (4)\tabularnewline 2. & $\sim\left(\sim p\vee q\right)\equiv p$ & & (3) et (2)\tabularnewline 3. & $\left(p\wedge\sim q\right)\equiv p$ & & (4)\tabularnewline 4. & $\left(\left(p\wedge\sim q\right)\supset p\right)\wedge\left(p\supset\left(p\wedge\sim q\right)\right)$ & & (4)\tabularnewline 5. & $\left(\sim\left(p\wedge\sim q\right)\vee p\right)\wedge\left(\sim p\vee\left(p\wedge\sim q\right)\right)$ & & (3) et (2)\tabularnewline 6. & $\left(\left(\sim p\vee q\right)\vee p\right)\wedge\left(\sim p\vee\left(p\wedge\sim q\right)\right)$ & & (1)\tabularnewline 7. & $\left(\sim p\vee q\vee p\right)\wedge\left((\sim p\vee p)\wedge\left(\sim p\wedge\sim q\right)\right)$ & & \tabularnewline \end{tabular}

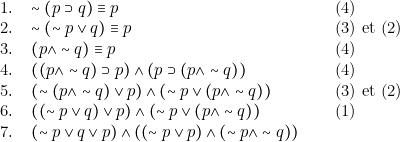
On constate que, au moment où aucune des règles (1) à (4) n’est plus applicable,
1) l’expression obtenue a la forme d’une conjonction,
2) chaque facteur est une disjonction qui n’est pas nécessairement une disjonction élémentaire, en ce sens que tous les atomes n’y figurent pas toujours,

3) les signes de négation ne portent que sur les atomes. Toute proposition qui jouit de ces trois propriétés est une \emph{forme normale conjonctive}. On dira, dans l’exemple précédent, que \sim(p\supset q)\equiv p a été mise sous fnc

Considérons maintenant le cas d’une tautologie, disons (p\wedge(p\supset q))\supset q.

Mettons-la sous \textsc{fnc} :

\begin{tabular}{clcl} 1. & $(p\wedge(p\supset q))\supset q$ & & (4)\tabularnewline 2. & $\sim\left(p\wedge\left(\sim p\vee q\right)\right)\vee q$ & & (3) \tabularnewline 3. & $\left(\sim p\vee\sim\left(\sim p\vee q\right)\right)\vee q$ & & (3) et (2)\tabularnewline 4. & $\left(\sim p\vee\left(p\wedge\sim q\right)\right)\vee q$ & & (1)\tabularnewline 5. & $(\left(\sim p\vee q\right)\wedge\left(\sim p\vee\sim q\right))\vee q$ & & (1)\tabularnewline 6. & $\left(\sim p\vee p\vee q\right)\wedge\left(\sim p\vee\sim q\vee q\right)$ & & (1)\tabularnewline \end{tabular}

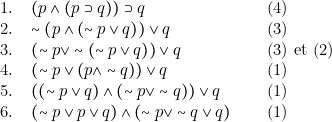
On constate que la fnc  existe, ce qui sera toujours le cas, puisque aucune des règles qui l’engendrent ne permet de faire disparaître un atome. De plus chacune des disjonctions contient un atome et sa négation. Cela fait que chaque disjonction a la valeur 1 et que la fnc, qui est une conjonction, a aussi la valeur 1.

Les seize opérateurs binaires
 		Le groupe I, N, R, D
Page suivante