La logique des propositions inanalysées |
L’idée naïve de déduction
Un exemple de déduction
Nous allons chercher, dans ce premier chapitre, à dégager un certain nombre de règles de déduction et à les exprimer de façon précise et commode. Partons pour cela d’une déduction simple, telle qu’elle se présente dans le discours quotidien.
« Si le ciel se couvre, il ne gèlera pas et s’il ne gèle pas, le chien peut rester dehors pour la nuit. Le ciel se couvre. Donc le chien pourra rester dehors ».
Il faut tout d’abord remarquer que, d’un point de vue tout extérieur, nous avons affaire à une suite de propositions. Cherchons donc à les énumérer. Nous nous heurtons immédiatement à une difficulté : certaines sont au présent, d’autres au futur. Faut-il compter « il ne gèlera pas » comme une proposition et « il ne gèle pas » comme une autre ou, au contraire, puisque toutes deux ont trait au même fait, faut-il n’en compter qu’une ? D’autre part, « le chien peut rester dehors pour la nuit » contient deux verbes, « peut » et « rester ». S’agit-il d’une ou de deux propositions ?
Ces quelques remarques montrent que, aussitôt que l’on s’efforce de tirer au clair des procédures pourtant familières, on se met dans l’obligation d’effectuer certains choix plus ou moins arbitraires et d’effectuer un certain nombre de simplifications. Le fait est d’importance, en ce sens qu’il manifeste l’autonomie du système que l’on a l’intention de construire. En droit, en effet, nous sommes entièrement libres de nous donner les règles de déduction que nous voulons. De même que le géomètre, qui crée des êtres abstraits à l’aide de ses lignes sans épaisseur et de ses points sans dimension, peut les doter des propriétés qui lui plaisent, de même nous pouvons, si nous le voulons, attribuer aux objets abstraits que nous allons appeler des propositions n’importe quelles propriétés. Toutefois ce n’est encore qu’un aspect de la situation. Le géomètre souhaite que les objets qu’il crée puissent admettre certains modèles concrets (des figures dessinées à l’encre, par exemple). Quant à nous, nous désirons que ce que nous nommerons « propositions » ait quelque chose à voir avec les propositions que nous énonçons en parlant chaque jour.
C’est la raison pour laquelle notre démarche, dans ce premier chapitre, sera la suivante :
1. Examiner certains emplois attestés,
2. En retenir quelques-uns, soit que nous les supposions particulièrement importants en pratique, soit qu’ils conviennent à notre construction pour des raisons propres au logicien,
3. Oublier l’origine pratique de notre choix et nous en tenir strictement à ce que nous aurons posé,
4. Interpréter le système obtenu dans les termes concrets qui lui auront servi d’origine.
Dans la construction de la géométrie, le point 1 correspond à l’examen quasi-physique des propriétés des objets, plus ou moins bien dessinés ; le point 2 au choix des axiomes et des postulats ; le point 3 au déroulement du système de la géométrie et le point 4, enfin, à l’application de la géométrie à la réalité concrète.
Ceci dit, nous allons prendre notre première décision en postulant que nous ne tiendrons pas compte des diverses formes des verbes, non plus d’ailleurs que d’autres différences stylistiques qui pourraient se présenter. En fait, notre décompte sera sensiblement celui des « phrases-noyaux » de Chomsky.
Reste la question de savoir comment découper les propositions. Puisque, à ce stade, nous procédons intuitivement, donnons-nous un critère, lui aussi intuitif. Sera réputée proposition unique, celle qui est susceptible d’être dite vraie ou fausse. Ainsi, il n’y a aucun sens à dire que « le chien peut » est vraie ou fausse, tandis qu’il y en a un à le dire de « le chien peut rester dehors pour la nuit ». Cette dernière expression sera donc comptée comme une seule proposition.
Finalement nous aurons donc affaire à trois propositions, que nous allons abréger par les lettres 
, 
et 
:
: le ciel se couvre
: il ne gèle pas
: le chien peut rester dehors pour la nuit.
La déduction prend alors la forme abrégée suivante : « Si alors et si alors . . Donc .~»
Nous voyons maintenant qu’il est possible de partager nos propositions en deux espèces. Les unes sont simples : , . Les autres sont composées : si alors et si alors . Nous appellerons les premières des propositions atomiques et les secondes des propositions composées ou moléculaires . Mais composées comment ? On le voit : à l’aide de propositions atomiques (, et ) et des mots « si … alors » et « et ».
Remarque
| Le caractère atomique d’une proposition est relatif et dépend largement des décisions que l’on prend. Ainsi, nous avons décidé de considérer « il ne gèle pas » comme un atome. Mais rien ne nous aurait empêché de choisir « il gèle » pour atome et de faire de « il ne gèle pas », donc de « non il gèle » une proposition moléculaire, composée de la négation « non » et de l’atome « il gèle ». |
Reste à nous occuper du caractère déductif de l’exemple. Pour mieux le faire ressortir, écrivons les choses comme suit :
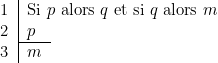
Les propositions 1 et 2, séparées de la proposition 3 par une petite barre horizontale, constituent les hypothèses de la déduction. La proposition 3 en est la conclusion . La ponctuation, qui séparait « si alors et si alors m » de « » et « » de « Donc » n’est ici plus nécessaire, puisque les propositions sont écrites individuellement les unes au-dessous des autres. Quant au mot « Donc », il est représenté par la petite barre horizontale.
Remarque
On dit aussi que est déduite de la classe d’hypothèses si alors et si alors , .