Étude d'un exemple. |
Considérons la situation suivante :
C’est l’été, je me promène. Une averse a mouillée la chaussée. Dans quels cas me mouillerai-je sachant que : il peut continuer à pleuvoir ou non ; si j’ai un parapluie, j’admets qu’il m’abrite de la pluie ; si j’ai des chaussures aux pieds, j’admets que j’ai les pieds sec.
- Désignons par A, B, C, les trois propositions suivantes :
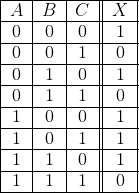
A « il continue de pleuvoir » (vrai ou faux) ; B « j’ai un parapluie » (vrai ou faux) ; C « j’ai des chaussures aux pieds » (vrai ou faux) ; Il y a donc 8 possibilités, indiquées par la table de valeurs ci-dessous (faux : 0 ; vrai : 1).
Soit X la proposition : « je me mouille » (vrai ou faux). Le problème consiste à connaître tous les cas pour lesquels X prend la valeur 1.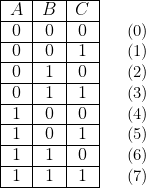
- Étudions tous les cas possibles.
- — Première ligne :
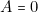 ,
, 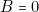 ,
, 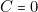 , c’est-à-dire « il ne pleut plus et je n’ai pas de parapluie et je n’ai pas de chaussures aux pieds ». Il est alors clair, la chaussée étant mouillée, que je me mouille des lieds, donc
, c’est-à-dire « il ne pleut plus et je n’ai pas de parapluie et je n’ai pas de chaussures aux pieds ». Il est alors clair, la chaussée étant mouillée, que je me mouille des lieds, donc 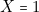 . Or (
. Or (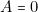 ) et (
) et (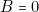 ) et (
) et (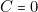 ) correspond à
) correspond à 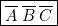 (d’après la première partie, paragraphe 2 et 3).
(d’après la première partie, paragraphe 2 et 3). - — Deuxième ligne :
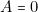 ,
, 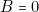 ,
, 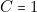 c’est-à-dire : « il ne pleut plus et je n’ai pas de parapluie et j’ai des chaussures aux pieds ». Dans ce cas, je ne me mouille pas ; donc
c’est-à-dire : « il ne pleut plus et je n’ai pas de parapluie et j’ai des chaussures aux pieds ». Dans ce cas, je ne me mouille pas ; donc 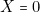 .
. - — Troisième ligne :
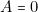 ,
, 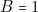 ,
, 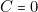 c’est-à-dire : « il ne pleut plus et j’ai un parapluie et je n’ai pas de chaussures aux pieds ». La chaussée étant mouillée, il est clair que … je me mouille les pieds. Par suite
c’est-à-dire : « il ne pleut plus et j’ai un parapluie et je n’ai pas de chaussures aux pieds ». La chaussée étant mouillée, il est clair que … je me mouille les pieds. Par suite 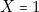 . Remarquons que cela correspond à la proposition
. Remarquons que cela correspond à la proposition 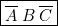 (voir première partie, §2 et 3).
(voir première partie, §2 et 3). - — Quatrième ligne :
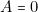 ,
, 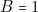 ,
, 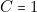 . On montre que
. On montre que 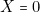 , c’est à dire que je ne me mouille pas.
, c’est à dire que je ne me mouille pas. - — Cinquième ligne :
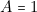 ,
, 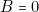 ,
, 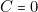 c’est à dire : « il continue de pleuvoir et je n’ai pas de parapluie et je n’ai pas de chaussures aux pieds ». Donc …je me mouille, soit
c’est à dire : « il continue de pleuvoir et je n’ai pas de parapluie et je n’ai pas de chaussures aux pieds ». Donc …je me mouille, soit 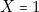 . Ceci correspond à la proposition
. Ceci correspond à la proposition 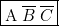
- — Sixième ligne :
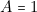 ,
, 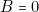 ,
, 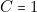 . Il est immédiat que
. Il est immédiat que 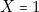 (je me mouille…) Cela correspond à la proposition
(je me mouille…) Cela correspond à la proposition 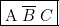
- Septième ligne :
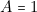 ,
, 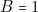 ,
, 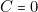 c’est à dire « il continue de pleuvoir et j’ai un parapluie et je n’ai pas de chaussures aux pieds ». Donc…
c’est à dire « il continue de pleuvoir et j’ai un parapluie et je n’ai pas de chaussures aux pieds ». Donc… 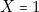 (je ne me mouille pas les pieds). Ce cas correspond à la proposition
(je ne me mouille pas les pieds). Ce cas correspond à la proposition 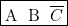
- — Huitième ligne :
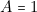 ,
, 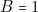 ,
, 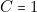 . Il est calir que je ne me mouille pas (
. Il est calir que je ne me mouille pas (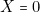 ).
D’où la table des valeurs c-contre.
).
D’où la table des valeurs c-contre.
- — Première ligne :
- Quelle est la proposition X ?
« Je me mouille » dans l’un au moins des cinq cas indiqués ci-dessus (lignes 1, 3, 5, 6, 7). Donc (voir première partie, §4) : ![Rendered by QuickLaTeX.com \[ X = \left|\begin{array}{ccc} \overline{A} & \overline{B} & \overline{C} \\ \overline{A} & B & \overline{C} \\ A & \overline{B} & \overline{C} \\ A & \overline{B} & C \\ A & B & \overline{C} \\ \end{array}\right| \]](https://jr01.dhenin.fr/wp-content/ql-cache/quicklatex.com-fd22e961330ecd10d0dbde5daf4d5f42_l3.png)
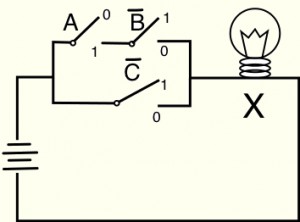
Montages électriques.
Le circuit électrique correspondant à cette proposition serait le suivant (voir 1ere partie). (Ne pas oublier qu’un montage en série correspond à et et un montage en parallèle à ou)
Ce montage est compliqué.
Or les règles de calcul présenté dans la première partie (§7) permettent de remplacer l’expression de X par une autre équivalente mais plus simple. Il en résultera une simplification du circuit électrique correspondant.
En effet :
![Rendered by QuickLaTeX.com \[ X = \left|\begin{array}{c} \overline{A} \; \overline{B} \; \overline{C} \\ \overline{A} \; B \; \overline{C} \\ A \; \overline{B}\; \overline{C} \\ A \; \overline{B} \; C \\ A \; B \; \overline{C} \\ \end{array}\right| \]](https://jr01.dhenin.fr/wp-content/ql-cache/quicklatex.com-6f3de3f732d5fcbba155099d50ee7c7e_l3.png)
et, d’après la première partie, §7, formule (5) :
![Rendered by QuickLaTeX.com \[ X = \left| \begin{array}{c} \begin{array}{cc|c|} \multicolumn{2}{c|}{\multirow{2}{*}{$\overline{A} \; \overline{C}$}} & \overline{B} \\ & & B \\ \end{array} \\ \begin{array}{c|c|} \multirow{3}{*}{A} & \overline{B}\;\overline{C}\\ & \overline{B} \; C \\ & B \; \overline{C} \\ \end{array} \\ \end{array}\right| \]](https://jr01.dhenin.fr/wp-content/ql-cache/quicklatex.com-b24aa101efc4d3800dbed72e6f0e6011_l3.png)
et, d’après la première partie, §6 et 7, formule (12) et (10) :
![Rendered by QuickLaTeX.com \[ X = \left| \begin{array}{@{}c} \overline{A}\;\overline{C}\\ \begin{array}{c|c|} \multirow{2}{*}{A} & \overline{B}\\ & \overline{C} \\ \end{array} \\ \end{array} \right| \]](https://jr01.dhenin.fr/wp-content/ql-cache/quicklatex.com-a4f2d1f1ad996f31a4f13f92286eb2f3_l3.png)
et, d’après première partie, § 6 et 7, formule (5) :
![Rendered by QuickLaTeX.com \[ X = \left| \begin{array}{c} \overline{A}\;\overline{C}\\ A \;\overline{B}\\ A\;\overline{C}\\ \end{array} \right| = \left| \begin{array}{@{}c} \overline{A}\;\overline{B}\\ \begin{array}{c|c|} \multirow{2}{*}{$\overline{C}$} & \overline{A}\\ & A\\ \end{array} \\ \end{array} \right| \]](https://jr01.dhenin.fr/wp-content/ql-cache/quicklatex.com-900ec5dfe69c205d443b26c635c45185_l3.png)
en définitive :
![]()
Ce qui signifie « je me mouille » si :
« (il pleut et je n’ai pas de parapluie)
ou (je n’ai pas de chaussures aux pieds) »
Le circuit électrique correspondant est alors extrêmement simplifié :
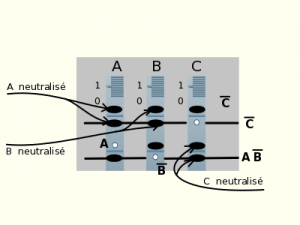
- Comment, alors, programmer l’ordinateur J.R. 01 ? C’est extrêmement simple.
1° Il nous faut deux branches en parallèles, à savoir : celle de ![]() et celle de
et celle de ![]() . Ces branches doivent être reliées à une sortie. Choisissons (ce n’est pas une obligation) de lire les résultats sur la lampe X. Donc on va relier X à deux « branches ».
. Ces branches doivent être reliées à une sortie. Choisissons (ce n’est pas une obligation) de lire les résultats sur la lampe X. Donc on va relier X à deux « branches ».
2° Choisissons de porter ![]() sur la première ligne. Pour cela :
sur la première ligne. Pour cela :