La relation d’implication et celle d’équivalence

Proposition disjonctive

 La négation
Page suivante

Une proposition disjonctive est de la forme P ou Q et nous noterons : P\vee Q. Il est d’autant plus remarquable de constater que la quasi-totalité des logiciens est d’accord aujourd’hui pour utiliser le signe \vee que la conjonction (grammaticale) ou peut avoir deux sens. Elle peut indiquer la disjonction exclusive ou le disjonction non exclusive.

1) Disjonction exclusive. On entend que l’une seulement des propositions est vérifiée.

Exemple : « Tu mangeras ta soupe ou tu seras privé de dessert. » Le contexte familial et normal laisse entendre que si l’enfant mange sa soupe, il aura du dessert. C’est l’usage qui correspond au latin aut.

2) Disjonction non exclusive. Ici on admet que les deux propositions peuvent être satisfaites. Ceci correspond au latin vel et, en anglais scientifique, on écrit parfois and/or.

Exemple : « Le roi, l’âne ou moi nous mourrons », proposition qui peut se paraphraser :

« Le roi mourra ou l’âne mourra ou je mourrai », sans qu’il soit exclu que plus d’un malheur se produise.


Pour des raisons purement internes au système que nous élaborons, et sur lesquelles nous reviendrons plus loin (Fascicule 2), nous allons nous donner des règles qui conduisent à l’interprétation non exclusive.

Supposons donc que quelqu’un ait pu établir la proposition P et donc que, en un sens naïf, P soit vraie. Dans ces conditions, P\vee Q sera aussi vraie. En effet deux cas sont possibles~ :

1) Q est une proposition fausse. Mais le sens de ou est précisément d’exprimer qu’il suffit que l’une des deux propositions soit vérifiée.
2) Q est une proposition vraie. Dans ce cas les deux propositions sont vraies, ce qui est admissible dans l’interprétation non exclusive que nous avons choisie.

Nous poserons alors :

Règle \boldsymbol{\vee} e

\begin{tabular}{c|ll} $n$ & $P$ & \\ & \ldots{} & \\ & $P\vee Q$ & $n$, $\vee$ i\\ \end{tabular}\hspace*{1cm}% \begin{tabular}{c|ll} $n$ & $Q$ & \\ & \ldots{} & \\ & $P\vee Q$ & $n$, $\vee$ i\\ \end{tabular}

Comme on le voit, la règle se présente sous deux formes. La première permet d’introduire une proposition à droite de celle donnée à la ligne n, la seconde d’introduire une proposition à gauche de celle donnée à la ligne n. Il ne semble pas plus nécessaire ici que dans le cas de la règle \wedge e d’introduire deux sigles distincts.

Exemples

[1] \vdash p\supset(p\vee p)

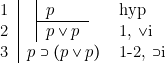
\begin{tabular}{c|c|lcl} 1 & & $p$ & & hyp\\ \cline{3-3} 2 & & $p\vee p$ & & 1, $\vee$i\\ 3 & \multicolumn{3}{l}{$p\supset(p\vee p)$} & 1-2, $\supset$i\\ \end{tabular}

[2] \vdash p\supset(p\vee q)
\begin{tabular}{c|c|lcl} 1 & & $p$ & & hyp\\ \cline{3-3} 2 & & $p\vee q$ & & 1, $\vee$ i\\ 3 & \multicolumn{3}{l}{$p\supset(p\vee q)$} & 1-2, $\supset$i\\ \end{tabular}


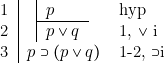
Remarque

L’exemple [1] permet d’écrire p\rightarrow p\vee p, soit de dire que p implique p\vee p. Ceci n’a rien de particulièrement choquant. En revanche, l’exemple [2] conduit à affirmer que p implique (logiquement) p ou q, soit p ou n’importe quelle proposition. Et ce fait peut paraître plus gênant. Nous ne saurions recommander à un candidat bachelier de répondre que « toute équation du deuxième degré a deux solutions ou qu’elle en a vingt et une ». Néanmoins, la règle \veei et l’algèbre (une équation du deuxième degré a deux solutions, réelles ou pas) s’accordent pour faire de la proposition disjonctive ci-dessus une proposition vraie. Cet exemple laisse entendre que notre façon de traiter le foncteur « ou » (et d’ailleurs les autres foncteurs logiques) ne tient aucun compte de l’information transmise par les propositions (Voir au Fascicule 2 la notion de tautologie).

Pour éliminer \vee, nous poserons en règle une pratique assez fréquente et qu’illustre l’exemple suivant.

Supposons qu’on sache d’un triangle qu’il est isocèle ou équilatéral.

Nous pourrons alors raisonner ainsi :

\begin{tabular}{lll} {\it 1ère hypothèse} : & 1. Le triangle est isocèle. & \\ & 2. Il a deux angles égaux. & 1, raison. géom.\\ {\it 2ème hypothèse} : & 3. Le triangle est équilatéral, & \\ & 4. Il a deux angles égaux. & 3, raison. géom.\\ \end{tabular}

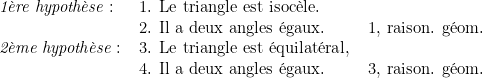
Donc, puisque nous savons que le triangle en question est « isocèle ou équilatéral » et que chacun des termes de l’alternative conduit à la même conclusion, nous pouvons affirmer que ce triangle a deux angles égaux (au moins).

Nous poserons alors :

Règle \boldsymbol{\vee} e

\begin{tabular}{c|l|lcl} n & \multicolumn{2}{l}{$P\vee Q$} & & \\ & \multicolumn{1}{l}{\ldots{}} & & & \\ $m$ & & $P$ & & hyp\\ \cline{3-3} & & $\cdot$ & & \\ & & $\cdot$ & & \\ $m^{'}$ & & $M$ & & \\ & \multicolumn{1}{l}{} & & & \\ $l$ & & $Q$ & & hyp\\ & & $\cdot$ & & \\ & & $\cdot$ & & \\ $l^{'}$ & & $M$ & & \\ & \multicolumn{1}{l}{$M$} & & & $n,m--m',l--l',\vee$e\\ \end{tabular}

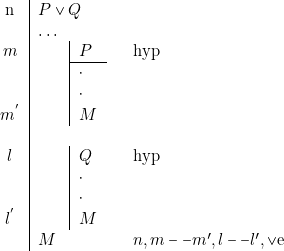
Cette règle exige donc de poser successivement comme hypothèse chacun des termes de la proposition disjonctive P\vee Q. Elle conduit donc à faire deux sous-déductions et à tenter de déduire (par les règles du système) une même proposition M. Si on y parvient, la règle \veee autorise à écrire M dans la même déduction que P\vee Q. Il faut noter encore que les deux sous-déductions sont indépendantes l’une de l’autre. En particulier, ni la règle rep, ni la règle reit ne permet de répéter une proposition de l’une dans l’autre.

[3] \vdash p\vee q\cdot\supset\cdot q\vee p

\begin{tabular}{c|l|l|lccl} 1 & & \multicolumn{3}{l}{$p\vee q$} & & hyp (pour introduire $\supset$)\\ \cline{3-3} 2 & & & $p$ & & & hyp (pour introduire $\vee$)\\ \cline{4-4} 3 & & & \multicolumn{2}{l}{$p\vee q$} & & 2, $\vee$i (deuxième forme)\\ & & \multicolumn{1}{l}{} & & & & \\ 4 & & & q & & & hyp (second terme de l'alternative)\\ \cline{4-4} 5 & & & \multicolumn{2}{l}{$p\vee q$} & & 4, $\vee$i (première forme)\\ 6 & & \multicolumn{3}{l}{$p\vee q$} & & 1, 2-3, 4-5, $\vee$e\\ & \multicolumn{3}{l}{Th.} & & & 1-6, $\supset$i\\ \end{tabular}

Remarque

Comme on peut démontrer, de façon analogue, la réciproque de ce théorème, on peut conclure que l’opération de disjonction est commutative. %

[4] \vdash p\vee p\cdot\supset p

\begin{tabular}{c|l|l|lcl} & & \multicolumn{3}{l}{$p\vee p$} & hyp\\ \cline{3-3} & & & $P$ & & hyp\\ \cline{4-4} & & & $P$ & & 2, rep\\ & & \multicolumn{1}{l}{} & & & \\ & & & $P$ & & hyp\\ \cline{4-4} & & & $P$ & & 4, rep\\ & & \multicolumn{1}{l}{$P$} & & & 1, 2-3, 4-5, $\vee$e\\ & \multicolumn{3}{l}{Th.} & & 1-6, $\supset$i\\ \end{tabular}
Remarques

1) Cet exemple, dont la démonstration pourrait en pratique être abrégée puisque les lignes 4 et 5 ne sont que la répétition des lignes 2 et 3, souligne assez bien l’aspect ludique du système. 2) Les exemples (1) et (4) permettent de dire que l’opération y est idempotente. 3) On établira, en exercice, qu’elle est aussi associative. La manipulation de la disjonction étant un peu moins facile que celle des autres opérations, nous allons encore en donner deux exemples.


[5] \vdash p\vee\left(q\wedge m\right)\cdot\supset\cdot\left(p\vee q\right)\wedge\left(p\vee m\right)


\begin{tabular}{r|l|l|lccl} 1 & & \multicolumn{3}{l}{$p\vee\left(q\wedge m\right)$} & & hyp \\ \cline{3-3} 2 & & & $p$ & & & hyp (pour éliminer $\vee$ dans 1\\ \cline{4-4} 3 & & & \multicolumn{2}{l}{$p\vee q$} & & 2, $\vee$i \\ 4 & & & \multicolumn{2}{l}{$p\vee m$} & & 2, $\vee$i \\ 5 & & & \multicolumn{2}{l}{$\left(p\vee q\right)\wedge\left(p\vee m\right)$} & & 3, 4 $\wedge$i\\ & & \multicolumn{1}{l}{} & & & & \\ 6 & & & \multicolumn{2}{l}{$q\wedge m$} & & hyp (pour éliminer $\vee$ dans 1\\ \cline{4-4} 7 & & & $q$ & & & 6, $\wedge$e\\ 8 & & & $m$ & & & 6, $\wedge$e\\ 9 & & & \multicolumn{2}{l}{$p\vee q$} & & 7, $\vee$i\\ 10 & & & \multicolumn{2}{l}{$p\vee m$} & & 8, $\vee$i\\ 11 & & & \multicolumn{2}{l}{$\left(p\vee q\right)\wedge\left(p\vee m\right)$} & & 4, $\vee$i (première forme)\\ 12 & & \multicolumn{3}{l}{$\left(p\vee q\right)\wedge\left(p\vee m\right)$} & & 1, 2-5, 6-11, $\vee$e\\ 13 & \multicolumn{4}{l}{Th.} & & 1-12, $\supset$i\\ \end{tabular}


[6] \vdash\left(p\vee q\right)\wedge\left(p\vee m\right)\cdot\supset\cdot p\vee\left(p\wedge m\right)


\begin{tabular}{r|l|l|l|cccl} 1 & & \multicolumn{4}{l}{$\left(p\vee q\right)\wedge\left(p\vee m\right)$} & & hyp \\ \cline{3-6} 2 & & \multicolumn{4}{l}{$p\vee q$} & & 1, $\wedge$e\\ 3 & & \multicolumn{4}{l}{$p\vee m$} & & 1, $\wedge$e\\ 4 & & & \multicolumn{1}{l}{$p$} & \multicolumn{2}{c}{} & & hyp (pour éliminer $\vee$ dans 2)\\ \cline{4-4} 5 & & & \multicolumn{3}{l}{$p\vee(q\wedge m)$} & & 4, $\vee$i\\ & & \multicolumn{4}{l}{} & & \\ 6 & & & \multicolumn{3}{l}{$q$} & & hyp (pour éliminer $\vee$ dans 2)\\ 7 & & & \multicolumn{3}{l}{$p\vee m$} & & 3, reit\\ 8 & & & & $p$ & & & hyp (pour éliminer $\vee$ dans 7)\\ \cline{5-5} 9 & & & & \multicolumn{2}{l}{$p\vee\left(q\wedge m\right)$} & & 8, $\vee$i\\ & & \multicolumn{4}{l}{} & & \\ 10 & & & & $m$ & & & hyp (pour éliminer $\vee$ dans 7)\\ \cline{5-5} 11 & & & & $q$ & & & 6, reit\\ 12 & & & & \multicolumn{2}{l}{$q\wedge m$} & & 10, 11, $\wedge$i\\ 13 & & & & \multicolumn{2}{c}{$p\vee\left(q\wedge m\right)$} & & 12, $\vee$i\\ 14 & & & \multicolumn{3}{l}{$p\vee\left(q\wedge m\right)$} & & 7, 8-9, 10-13, $\vee$e\\ & & \multicolumn{4}{l}{$p\vee\left(q\wedge m\right)$} & & 2, 4-5, 6-14, $\vee$e\\ 13 & \multicolumn{4}{l}{Th.} & & & 1-125, $\supset$i\\ \end{tabular}


Remarque


L’équivalence p\vee\left(q\wedge m\right)\longleftrightarrow\left(p\vee q\right)\wedge\left(p\vee m\right) exprime la distributivité de \vee par rapport à \wedge. On verra en exercice que la distributivité de \wedge par rapport à \vee peut aussi être établie.

La relation d’implication et celle d’équivalence
 		La négation
Page suivante