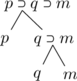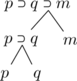La proposition conditionnelle |
Nous appellerons (proposition) conditionnelle toute proposition de la forme
si ![]() alors
alors ![]() ,
,
étant entendu que P et Q désignent des propositions soit atomiques, soit moléculaires.
Exemples
[1] Si le nombre n est divisible par 6, alors il est pair.
[2] S’il pleut dimanche, le match n’aura pas lieu.
[3] « Il les condamne dans Jansénius, si elles y sont » (Pascal).
[4] S’il est vraiment courageux, alors si le fantôme apparaît, il s’en moquera.
[5] Si j’avais su, je ne serais pas venu !
[6] S’il réussit ses examens, je mange mon chapeau.
Les exemples [2] et [3] fournissent des variations linguistiques de « si … alors ». Mais il convient toujours de distinguer deux propositions :
– celle qui suit le mot « si », qui constitue l’antécédent de la conditionnelle,
– l’autre, qui en est le conséquent.
Au lieu d’écrire une proposition conditionnelle sous la forme : « si proposition antécédente, alors proposition conséquente », nous introduirons le signe « ⊃ ». Ainsi, en posant :
p =df il pleut dimanche
q =df le match n’aura pas lieu,
on aura pour l’exemple [2] : ![]() ⊃
⊃ ![]() .
.
Remarque
|
Certains auteurs écrivent |
Le quatrième exemple pose un problème. Si nous ne prêtons pas trop d’attention à la ponctuation, nous sommes enclins à l’écrire :
![]() ,
,
les lettres ![]() ,
, ![]() et
et![]() ayant une signification évidente. Sous cette forme cependant, la proposition est ambiguë. Il est en effet possible de l’analyser de deux façons :
ayant une signification évidente. Sous cette forme cependant, la proposition est ambiguë. Il est en effet possible de l’analyser de deux façons :
(a) ![]() où
où ![]() désigne
désigne ![]()
(b) ![]() où
où ![]() désigne
désigne ![]() .
.
Ces deux analyses correspondent aux arbres suivants :
| (a) |
|
(b) |
|
Pour lever de telles ambiguïtés, nous userons de parenthèses, sans d’ailleurs prendre ici la peine d’en fixer précisément le maniement (voir le Fascicule 3). Nous interpréterons l’exemple [4] de la façon suivante :
![]() ,
,
ce qui correspond donc à la forme (a).
Enfin, les exemples [5] et [6] apparaissent rapidement transmettre un tout autre genre d’information que les quatre premiers. Ceux-ci correspondent, très sommairement, à la situation suivante. On sait (ou on décide) que dans le cas où les circonstances décrites par l’antécédent ![]() se réaliseront, alors les circonstances décrites par le conséquent
se réaliseront, alors les circonstances décrites par le conséquent ![]() se réaliseront aussi. En revanche, on ne sait pas actuellement ce qu’il en est de
se réaliseront aussi. En revanche, on ne sait pas actuellement ce qu’il en est de ![]() et c’est même la raison pour laquelle on dit « si
et c’est même la raison pour laquelle on dit « si ![]() alors
alors ![]() ».
».
Il en va tout autrement pour l’exemple [5] où celui qui parle ne sait que trop que l’antécédent ![]() n’a pas été réalisé et dans l’exemple [6] où le locuteur s’attend si peu à ce que l’antécédent
n’a pas été réalisé et dans l’exemple [6] où le locuteur s’attend si peu à ce que l’antécédent ![]() se vérifie qu’il est disposé à promettre n’importe quoi.
se vérifie qu’il est disposé à promettre n’importe quoi.
Les règles que nous allons poser s’inspireront du premier usage de « si… alors » (exemples [1] à [4]) et nullement des deux autres. C’est ainsi que nous poserons, pour éliminer le signe « ![]() », la règle d’élimination suivante :
», la règle d’élimination suivante :
Règle ![]() e
e
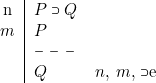
Le trait pointillé indique que les propositions numéros ![]() et
et ![]() ne sont pas nécessairement des hypothèses (au sens de la règle hyp), mais servent de prémisses à la règle
ne sont pas nécessairement des hypothèses (au sens de la règle hyp), mais servent de prémisses à la règle ![]() e. Cette règle est aussi classiquement nommée règle du modus ponens.
e. Cette règle est aussi classiquement nommée règle du modus ponens.
Exemples
![Rendered by QuickLaTeX.com \begin{tabular}{rr|lcl} [1] & 1 & $p\supset q$ & & hyp\tabularnewline & 2 & $q\supset m$ & & hyp\tabularnewline & 3 & $p$ & & hyp\tabularnewline \cline{3-3} & 4 & $q$ & & 1, 3, $\supset$e\tabularnewline & 5 & m & & 2, 4, $\supset$e\tabularnewline \end{tabular}\hfill{}% \begin{tabular}{cc|lcl} [2] & 1 & $p$ & & hyp\tabularnewline & 2 & $p\supset(p\supset q)$ & & hyp\tabularnewline \cline{3-3} & 3 & $p\supset q$ & & 2, 1, $\supset$e\tabularnewline & 4 & $q$ & & 3, 1, $\supset$e\tabularnewline \end{tabular}](https://jr01.dhenin.fr/wp-content/ql-cache/quicklatex.com-7404b469cabaa2a3e69dfe97c1204940_l3.png)
Dans les deux cas nous avons, en utilisant exclusivement les règles que nous nous sommes données, déduit une conclusion d’une classe d’hypothèses. Nous savons déjà que nous pouvons noter :
Ex. 1 ![]() est déduite de la classe d’hypothèses {
est déduite de la classe d’hypothèses { ![]() ,
, ![]() ,
, ![]() }
}
Ex. 2 ![]() est déduite de la classe d’hypothèses {
est déduite de la classe d’hypothèses { ![]() ,
, ![]() }
}
Il sera commode de noter les mêmes faits sous la forme abrégée suivante :
Ex. 1 ![]() ,
, ![]() ,
, ![]()
Ex. 2 ![]() ,
, ![]()
Examinons maintenant la façon d’introduire un signe et pour cela reprenons l’exemple [1]. Si quelqu’un cherche à établir la proposition conditionnelle « si le nombre n est divisible par 6, alors il est pair », il pourra procéder approximativement de la manière suivante :

Introduisant alors l’hypothèse faite et la conclusion obtenue \emph{dans une même proposition}, il dira : « Si le nombre n est divisible par 6, alors il est pair ».
Nous allons, quant à nous, accepter ce genre de procédure et poser, pour introduire un signe , la règle suivante :
\textbf{Règle ![]() i}
i}
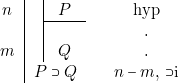
Le trait vertical de gauche indique que la règle est utilisable au cours d’une déduction quelconque. Le second trait vertical découle de l’application de la règle hyp, puisque pour introduire un « », il faut partir d’une hypothèse. Les petits points doivent être pensés comme indiquant les références. Mais, contrairement à ce qu’il se passait dans l’exemple, les références ne peuvent ici se faire qu’aux règles déjà posées ou à celles que nous poserons explicitement plus loin. Il faut enfin noter que la justification de la règle j ne fait pas mention seulement du point de départ (ligne n) et du point d’arrivée (ligne m), mais à toute la sous-déduction qui va de n à m. D’où la notation : n-m.
Remarque
| On appelle sous-déduction d’une déduction, toute suite de propositions accompagnées d’un trait vertical à droite d’un autre. |
Exemples
[1] ![]()

Remarque
|
Considérons la proposition |
On peut alors se demander s’il ne serait pas possible, dans certains cas, de se libérer de toute hypothèse. Voyons, pour cela, l’exemple suivant.
[2] ![]()

Remarques
|
1. Le trait de déduction qui est tout à gauche n’est marqué d’aucune petite barre horizontale. Donc la proposition 5 ne dépend d’aucune hypothèse. Il est vrai que, pour l’établir, nous avons dû recourir à des sous-déductions qui, elles, usaient d’hypothèses. Mais peu importe : la proposition 5 ne dépend directement d’aucune hypothèse, elle est déduite de la classe d’hypothèses vide. Nous écrirons : soit 2. Le premier trait vertical est indispensable~ : il indique que l’on effectue une déduction à partir de la classe d’hypothèses vide. On pourrait donc écrire aussi~ :
|
[3] ![]()
[4] ![]()
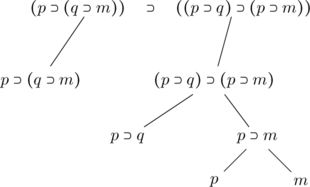
Pour trouver une démonstration de ce théorème, qui est déjà un peu compliqué, il suffit de procéder méthodiquement.
1. Comme tout théorème, il ne dépend d’aucune hypothèse, d’où le fait que le trait vertical numéro 0 n’a aucune barre horizontale.
2. Le théorème est de la forme ![]() , où
, où ![]() a la valeur
a la valeur ![]() et il nous faudra introduire ce premier signe
et il nous faudra introduire ce premier signe ![]() . Pour cela, la règle
. Pour cela, la règle ![]() i indique qu’il faut poser
i indique qu’il faut poser ![]() en hypothèse, en l’accompagnant d’un trait vertical (numéro 1).
en hypothèse, en l’accompagnant d’un trait vertical (numéro 1).
3. ![]() a la valeur
a la valeur ![]() , expression qui est encore de la forme
, expression qui est encore de la forme ![]() si on donne à
si on donne à ![]() la valeur
la valeur ![]() . Il nous faudra donc introduire ce second signe
. Il nous faudra donc introduire ce second signe![]() et poser, pour cela,
et poser, pour cela, ![]() en hypothèse, en l’accompagnant d’un trait vertical (numéro 2).
en hypothèse, en l’accompagnant d’un trait vertical (numéro 2).
4. Enfin Q’ a la valeur p m. Il ne reste plus qu’à nous mettre en situation pour introduire ce troisième signe « ». Pour cela on pose
p en hypothèse en l’accompagnant du trait vertical numéro 3.
5. Notre problème est maintenant d’utiliser les règles (et plus spécialement
6. la règle d’élimination) pour obtenir la proposition m (ligne 8). 6. Il suffit maintenant d’appliquer trois fois de suite la règle j pour reconstruire le théorème de proche en proche.
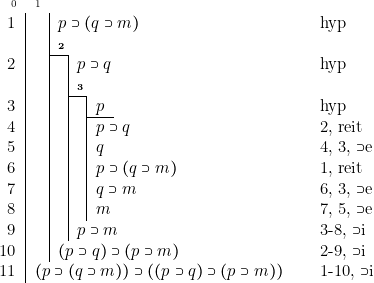
Remarques
|
1. II serait aussi possible d’analyser la proposition à démontrer sous forme d’arbre. On obtiendrait :
2. Le lecteur aura intérêt à examiner attentivement cet exemple, qui est paradigmatique.
Exemple :
4. On remarquera que, si une proposition contient plusieurs signes Exemple :
où |