La proposition biconditionnelle |
On rencontre souvent, dans les textes scientifiques, la locution « si et seulement si » que d’aucun abrègent en « ssi ».
Exemple : Un triangle a ses trois côtés égaux si il a ses trois angles égaux.
Un tel énoncé signifie deux choses :
1) Si un triangle a ses trois côtés égaux, il a ses trois angles égaux.
2) Si un triangle a ses trois angles égaux, il a ses trois côtés égaux.
La proposition qui contient « si et seulement si » équivaut donc à deux propositions conditionnelles. Nous la nommerons une proposition biconditionnelle et nous poserons la définition (notre première définition) :
Df 
: 
=df 
.
Remarques
|
1. Au lieu du foncteur abréviatif , certains auteurs notent  ou  .
2. II arrive fréquemment que, au vu du contexte, le langage courant se contente de « si\ldots{}alors », là où nous disons « ssi ». Exemple : Ouvrant son porte-feuille quelqu’un dit : « Si j’ai 10€ sur moi, je vous les prête ». Il va ici de soi que « Si je vous prête 10€, alors je les ai sur moi ». Il s’ensuit que chaque fois que l’on cherche à « traduire » un texte dans le formalisme logique, il faut être attentif, non seulement à l’expression adoptée, mais à sa signification. Certains raisonnements peuvent parfaitement être corrects avec et n’être pas valides avec  .
|
La règle repdf rend superflue l’introduction de règles spécifiques pour le foncteur .
Exemples
[1] Soit à démontrer le théorème 
. Cela signifie qu’il faut démontrer 
:
[2] 
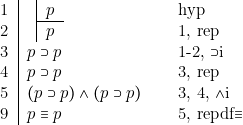
Pour des références ultérieures, notons encore :
[3] 
[4] 
[5] 