Une axiomatisation |
Nous allons construire un système formel pour la logique des propositions. Le « jeu » consiste à faire comme si l’on ne savait pas de quoi il s’agit, comme si les signes utilisés n’avaient pas de signification. Ce n’est que dans une seconde étape que l’on interprète les signes et l’on est alors en droit de dire que l’on a formalisé la logique des propositions, ou autre chose. Cela dépend de l’interprétation.
La première chose à faire est de se donner un alphabet. Le nôtre contiendra trois catégories de signes :
1) Les lettres ![]() ,
, ![]() , …
, … ![]() ,… . Nous les appellerons des variables de propositions.
,… . Nous les appellerons des variables de propositions.
Remarque
Cette appellation anticipe sur l’interprétation standard que nous avons en vue. Nous pourrions nous contenter de les appeler des variables, ou même des lettres.
2) Les signes ![]() et
et ![]() que nous appellerons des foncteurs.
que nous appellerons des foncteurs.
3) Les signes ( et ) que nous appellerons, comme tout le monde, des parenthèses.
Nous allons définir maintenant une classe qu’on nomme celle des expressions bien formées ou ebf.
1) Une variable est une ebf.
2) Si P est une ebf, ![]() est une ebf.
est une ebf.
3) Si ![]() et
et ![]() sont des ebf,
sont des ebf, ![]() est une ebf.
est une ebf.
4) Rien n’est une ebf, sinon par (1) à (3).
Une définition du genre ci-dessus est une définition inductive. Elle comporte trois sortes de clauses :
une ou plusieurs clause(s) initiale(s), ici (1) ;
une ou plusieurs clause(s) inductive(s), ici (2) et (3) ;
une clause terminale, ici (4).
Une telle définition permet d’engendrer de proche en proche autant d’éléments que l’on veut de la classe qu’elle définit. Pour éviter l’usage des indices nous poserons ![]() =df
=df ![]() ,
, ![]() =df
=df ![]() et
et ![]() =df
=df ![]() .
.
Exemples
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() sont des ebf.
sont des ebf.
La clause finale a l’air pédant. En fait, elle est d’une importance essentielle. Considérons en effet, la suite de signes ![]() . Elle est exclusivement constituée de signes de notre alphabet. On ne peut toutefois pas l’obtenir en appliquant les clauses (1) à (3). C’est la clause terminale (4) qui nous assure que, en conséquence, il ne s’agit pas d’une ebf.
. Elle est exclusivement constituée de signes de notre alphabet. On ne peut toutefois pas l’obtenir en appliquant les clauses (1) à (3). C’est la clause terminale (4) qui nous assure que, en conséquence, il ne s’agit pas d’une ebf.
Remarque
Ceci est général. Quelle que soit la suite donnée de signes de l’alphabet, nous sommes à même de décider, en un nombre fini d’essais, si cette suite est une ebf ou non. On dit que la classe des ebf est une \emph{classe décidable}.
L’écriture des ebf devient rapidement encombrante. Aussi allons-nous convenir de certaines abréviations. Soit l’ebf suivante :
![]()
Posons : ![]() =df
=df ![]() .
.
Il vient :
![]()
Posons : ![]() =df
=df ![]() donc
donc ![]() .
.
Il vient :
![]()
Posons : ![]() =df
=df ![]() .
.
Il vient :
![]()
Convenons enfin de ne pas toujours écrire la paire extérieure de parenthèses ; l’ebf initiale peut s’écrire :
![]()
Remarque
Ces jeux d’écriture formels ne réclament aucune réflexion, mais ils exigent beaucoup d’attention. Le lecteur aura intérêt à refaire lui-même les diverses transformations, ne serait-ce que pour s’assurer que le texte ne contient pas de coquilles !
Soit ![]() ,
, ![]() ,
, ![]() des ebf quelconques. Introduisons les trois expressions suivantes, que nous appellerons des schémas d’axiomes.
des ebf quelconques. Introduisons les trois expressions suivantes, que nous appellerons des schémas d’axiomes.
(A1) ![]()
(A2) ![]()
(A3) ![]()
On obtiendra des axiomes en spécifiant quelles ebf désignent les lettres ![]() ,
, ![]() et
et ![]() . A ce propos il faut noter deux choses :
. A ce propos il faut noter deux choses :
1) Dans un même schéma, la même majuscule doit désigner la même ebf.
2) Mais dans un même schéma, deux majuscules différentes peuvent désigner la même ebf.
Remarque
Ces deux pratiques sont conformes à l’usage algébrique. Soit ainsi l’expression ![]() . Si l’on attribue une valeur à
. Si l’on attribue une valeur à ![]() , disons 3, il faut écrire
, disons 3, il faut écrire ![]() . Mais rien n’empêche d’attribuer aussi la valeur 3 à
. Mais rien n’empêche d’attribuer aussi la valeur 3 à ![]() .
.
Voici quelques axiomes. Nous indiquons par la notation (An) : ![]() ebf que dans le schéma (An), la variable
ebf que dans le schéma (An), la variable ![]() désigne : l’ebf qui suit la barre oblique.
désigne : l’ebf qui suit la barre oblique.
![]() (Al) :
(Al) : ![]() ,
, ![]()
![]() (Al) :
(Al) : ![]() ,
, ![]()
![]() (A2) :
(A2) : ![]() ,
, ![]() ,
, ![]()
![]() (A3) :
(A3) : ![]() ,
, ![]()
Il reste enfin à se donner au moins une règle d’inférence.
Nous poserons :
(R1) De ![]() et de
et de ![]() , il est loisible d’inférer
, il est loisible d’inférer![]() .
.
Cela dit, la notion de théorème se définit comme suit :
1) Un axiome est un théorème.
2) Toute ebf qui résulte de deux théorèmes par l’application de la règle (R1) est un théorème.
3) Rien n’est un théorème, sinon par (1) et (2).
Exemples
Chacune des cinq ebf suivantes est un théorème.
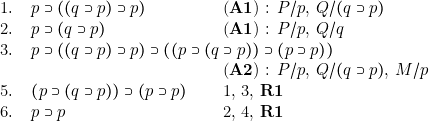
Remarques
1. Si ![]() est un théorème, nous écrirons encore
est un théorème, nous écrirons encore ![]() .
.
2. La classe des théorèmes est introduite par une définition inductive, comme celle des ebf. Nous verrons \eqref{sec :-Quelques-propri=0000E9t=0000E9s} qu’elle est aussi décidable. Toutefois ceci exige une démonstration.
3. Au lieu de se donner les schémas d’axiomes (A1 – A3), il serait possible de se donner directement des axiomes. Par exemple :
(a1) ![]()
(a2) ![]()
(a3) ![]()
Mais pour obtenir le même ensemble de théorèmes, il faudrait se donner une règle supplémentaire :
Si ![]() est une ebf qui contient la variable
est une ebf qui contient la variable ![]() et si
et si ![]() est une ebf, on peut inférer l’ebf que l’on obtient en substituant
est une ebf, on peut inférer l’ebf que l’on obtient en substituant ![]() à chaque mention de
à chaque mention de ![]() dans
dans ![]() . Cette façon de procéder est assez compliquée et elle exige de grandes précautions dans la logique des prédicats. C’est la raison pour laquelle nous ne l’avons pas adoptée.
. Cette façon de procéder est assez compliquée et elle exige de grandes précautions dans la logique des prédicats. C’est la raison pour laquelle nous ne l’avons pas adoptée.
Il est aussi possible de déduire des règles dérivées, ce qui est très commode pour la pratique. Convenons que si, à partir des prémisses ![]() ,
, ![]() ,… ,
,… ,![]() , il est possible d’inférer
, il est possible d’inférer ![]() , nous écrirons :
, nous écrirons :
![]() ,
, ![]() ,… ,
,… ,![]() .
.
Nous pourrions ainsi reformuler la règle (R1) de la façon suivante :
![]() ,
, ![]() .
.
Voici alors une règle dérivée :
![]() ,
, ![]() .
.
On a en effet :
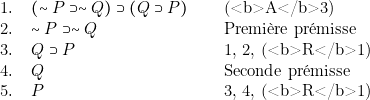
Un tel calcul n’offre d’intérêt réel qu’une fois interprété. Son interprétation standard est évidente :
  ; aux variables ![]() ,
, ![]() ,… ,
,… ,![]() on fait correspondre
on fait correspondre
des propositions ;
  ; aux signes ![]() et
et ![]() , on fait correspondre respectivement l’opérateur de négation et celui de conditionnel ;
, on fait correspondre respectivement l’opérateur de négation et celui de conditionnel ;
  ; les parenthèses.jouent le rôle de ponctuation.
Dès lors, si les schémas d’axiomes et la règle d’inférence sont bien choisis, aux théorèmes correspondront des tautologies (V. 1.7).
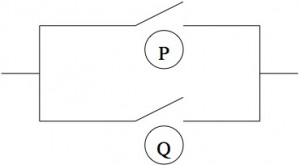
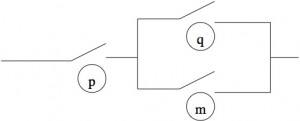
D’autres interprétations sont toutefois possibles. Nous allons en esquisser une, en interprétant les signes ![]() ,
, ![]() et
et ![]() . Supposons que p, q, m, représentent des interrupteurs électriques. Si p est fermé, il laisse donc passer le courant, nous écrivons
. Supposons que p, q, m, représentent des interrupteurs électriques. Si p est fermé, il laisse donc passer le courant, nous écrivons ![]() . Dans ce cas, à
. Dans ce cas, à ![]() correspond un montage en série (Fig. 4) et à
correspond un montage en série (Fig. 4) et à ![]() correspond un montage en parallèle (Fig. 5).
correspond un montage en parallèle (Fig. 5).
 |
 |
Nous avons noté ![]() et
et![]() les interrupteurs et non leur état.
les interrupteurs et non leur état.
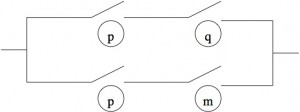
L’ebf suivante est un théorème du calcul :
![]()
Cela signifie que le montage de la figure 6 peut être remplacé par le montage de la figure 7.
 |
 |
Il est clair que les ordinateurs ne travaillent pas avec des interrupteurs mécaniques. Leurs principes logiques reposent bien toutefois sur une interprétation électrique du système précédent.
Remarque
L’axiomatisation que nous avons proposée est empruntée à Lukasiewicz. Elle n’est pas la seule possible. Ainsi dans leurs Principia Mathematica, Whitehead et Russell sont partis des opérateurs ![]() et
et ![]() et Nico du seul opérateur
et Nico du seul opérateur ![]() .
.
