Structures algébriques (bases)

L'analyse binaire, R.L. Vallée

 Transformations
Page suivante

Ensembles binaires algébriques

On appelle variable ou fonction binaire, toute variable ou toute fonction ne pouvant prendre que l’une des deux valeurs algébrique distinctes a \neq b, à l’exclusion de toute autre.

L’ensemble « E_{ab} » des variables et des fonctions ainsi définies est appelé ensemble binaire algébrique. Si l’élément « \phi_{ab} » est égal à « a » lorsqu’il est différent de « b » et s’il est égal à « b » lorsqu’il est différent  de « a », alors \phi_{ab} appartient à « E_{ab} ».

    \[ \phi_{ab} \in E_{ab} \mathrm{, si}\; (\phi_{ab} \neq a) \Rightarrow (\phi_{ab} = b) \mathrm{, et\;si,}\;(\phi_{ab} \neq b) \Rightarrow (\phi_{ab} = a) \]

Le choix de l’ensemble binaire E_{01} se justifie par l’adoption d’une valeur d’absorption « 0 » et d’une valeur neutre « 1 » qui font du produit algébrique une fonction binaire appartenant au même ensemble.

Produit

Soient n fonctions binaires f_{1}, f_{2}, \ldots f_{n} telles que f_{i} \in E_{01}, \forall i = 1, 2, \ldots n, le produit algébrique de ces n fonctions appartient à l’ensemble E_{01}.

    \[ (P=f_{1}.f_{2} \ldots f_{n}) \in E_{01} \]

Le produit P est en effet égal à l’unité lorsque toutes les fonctions en facteur sont simultanément égales à l’unité. (f_{1} = f_{2} = \ldots = f_{n} = 1) \Longleftrightarrow (P = 1).

Il est nul dans tous les autres cas.

Nous appellerons également le produit « P » fonction « ET » quand il fera l’objet d’application technologiques.

Produel

Il faut choisir un symbolisme simple qui puisse traduire dans l’expression écrite, la dualité qui caractérise les ensembles binaires et qui permette, en utilisant si possible les deux dimensions du plan, l’établissement de relations duales élémentaires.

Nous savons aussi, par dualité, qu’il est possible de faire correspondre au produit, la fonction algébrique binaire :

    \[ \pi=1-P \]

    \[\pi=1-(1-f_{1}).(1-f_{2}) \ldots (1-f_{n})=\overline{f_{1}.f_{2} \ldots f_{n}} \]

    \[f_{i}\in E_{01}, \forall i=1, 2, \ldots n) \Longrightarrow (\pi \in E_{01})\]

La fonction \pi est égale à zéro lorsque toutes les fonction f_{i} sont simultanément nulles,

    \[ f_{1} = f_{2} = \ldots = f_{n} = 0) \Longrightarrow (\pi = 0) \]

et qu’elle est égale à l’unité dans tous les autres cas, puisqu’il suffit qu’une fonction f_{i} au moins soit égale à l’unité pour que le produit algébrique (1-f_{1}).(1-f_{2}) \ldots (1-f_{n}) soit nul ; ce qui entraîne \pi = 1.

Nous conviendrons alors de représenter la fonction « \pi », que nous appellerons « produel »\footnote{Les racines latines « pro » et « dualis » ont été choisies dans la constitution du néologisme « produel » pour marquer d'une part la nécessité de conserver la dualité dans les expressions binaires et aussi par analogie avec le mot « produit »}. en groupant les termes qui la composent suivant une colonne verticale par analogie avec l’écriture horizontale du produit, pour traduire dans le symbolisme, la propriété de dualité.

    \[ \pi = \begin{array}{|c|}f_{1}\\ f_{2}\\ \vdots\\ f_{n}\\ \end{array} = 1 - (1-f_{1}).(1-f_{2}) \ldots (1-f_{n}) = \overline{f_{1}.f_{2} \ldots F_{n}} \]

Nous appellerons également « \pi », fonction « OU » dans le cas des applications technologiques.

Définition d’une structure logique binaire

La structure logique binaire se caractérise essentiellement par les deux opérations fondamentales qui ont des propriétés réciproques. Les symboles peuvent représenter des ensembles, des partitions d’ensembles, des groupes, des classes ou des éléments, voire même des opérateurs.

Les deux opérations sont, à la fois, commutatives, associatives, réciproquement distributives et possèdent, toutes deux, la propriété d’idempotence ; ce qui permet d’écrire successivement les égalités suivantes :

{\scriptsize \begin{tabular}{|l|l|} \hline \multicolumn{1}{|c|}{\it Produit} & \multicolumn{1}{|c|}{\it Produel} \\ \hline & \\ $P=a.b.c$ & $ \begin{array}{rcl} \pi & = & \begin{array}{|c|} a \\ b \\ c \\ \end{array} \\ & = & 1 - (1-a).(1-b).(1-c) \\ \end{array} $ \\ -- élément neutre «~1~»~& -- élément neutre «~0~»~\\ \multicolumn{1}{|c|}{$(1.f) = f$}& \multicolumn{1}{|c|}{$\begin{array}{|c|}0\\f\\\end{array} = f $} \\ -- élément absorbant «~0~»~& -- élément absorbant «~1~»~\\ \multicolumn{1}{|c|}{$(0.f) = 0$} & \multicolumn{1}{|c|}{$\begin{array}{|c|}1 \\ f\\ \end{array} = 1 $} \\ -- commutatif : $\begin{array}{|c|}ab\\\end{array} =\begin{array}{|c|}ba\\\end{array} $ & -- commutatif : $\begin{array}{|c|} a \\ b \\ \end{array} = \begin{array}{|c|}b \\ a \\ \end{array}$ \\ -- associatif : $\begin{array}{|c|c||}a& bc\\\end{array} =\begin{array}{||c|c|}ba&c\\\end{array} =\begin{array}{|c|}cba\\\end{array} $ & -- associatif : $ \begin{array}{||c||} \multicolumn{1}{|c|} {a} \\ b \\ c \\ \end{array} = \begin{array}{||c||} b \\ a \\ \multicolumn{1}{|c|} {c} \\ \end{array} = \begin{array}{|c|} c \\ b \\ a \\ \end{array} $ \\ & --distributif : \\ -- distributif : $\begin{array}{|c|} ab \\ ac \\ d\\ \end{array} = \begin{array}{|c|} a\; \begin{array}{|c}b \\ c \\ \end{array} \\ d \\ \end{array} = \begin{array}{|c|} d \\ \begin{array}{c|} b \\ c\\ \end{array}\; a \\ \end{array} = \begin{array}{|c|} d \\ b \\ c \\ \end{array} \begin{array}{c|} d \\ a \\ \end{array} $ & $\begin{array}{|c|c|}a & a \\ b & c \\ \end{array} \begin{array}{c|}d \\ \end{array} = \begin{array}{|c|}a \\ bc \\ \end{array} = \begin{array}{|c} d \\ \end{array} \begin{array}{|c|} bc \\ a \\ \end{array} = \begin{array}{|c|} dbc \\ da\\ \end{array}$\\ -- idempotent : $\begin{array}{|c|} aa \ldots a \\ \end{array} = \begin{array}{|c|} a \end{array} $ & -- idempotent : $\begin{array}{|c|} a\\ a\\ \vdots \\ a\\ \end{array} = \begin{array}{|c|} a \\ \end{array} $ \\ \multicolumn{1}{|c|}{$P=\overbrace{a.a \ldots a}^{n} = a^{n}$} & \multicolumn{1}{|c|}{$\pi= \left.\begin{array}{|c|}a \\ a\\ \vdots \\ a \\ \end{array} \right\} n = 1 - (1-n)^{n}$} \\ \multicolumn{1}{|c|}{pour $a = 0, \quad (0)^{n}= 0 $} & \multicolumn{1}{|c|}{pour $a = 0, \quad \pi = 1 -(1)^{n} = 0 $} \\ \multicolumn{1}{|c|}{pour $a = 1, \quad (1)^{n}= 1 $} & \multicolumn{1}{|c|}{pour $a = 1, \quad \pi = 1 -(1)^{n} = 1 $} \\ \multicolumn{1}{|l|}{ \begin{minipage}[t]{7.5cm} Si dans un produit, deux facteurs sont complémentaires, le produit est nul. \end{minipage} } & \multicolumn{1}{|l|}{ \begin{minipage}[t]{6cm} Si dans un produel, deux facteurs duals sont complémentaires, le produel est égal à l'unité \end{minipage} } \\ $P=f.\overline{f}.P_{1}$ & $ \pi = \begin{array}{|c|}f \\ \overline{f} \\ \pi _{1}\\\end{array} = 1 -(1-f).f.(1-\pi _{1}) $ \\ $ P = f.(1-f)P_{1} = (f - f^{2}). P_{1} $ & $ = 1 - (f - f^{2}).(1-\pi _{1}= 1 - 0 . (1- \pi _{1}) $ \\ $P=(0.P_{1}) = 0 $ & $ \pi = \begin{array}{|c|} 1 \\ \pi _{1} \\ \end{array} = 1 $ \\ $(f.\overline{f}) = 0 $ & $ \begin{array}{|c|} f \\ \overline{f} \\ \end{array} = 1 $ \\ \hline \end{tabular} }

Théorème de De Morgan

Ce théorème est contenu implicitement dans les définitions précédentes.

    \[ 1-\begin{array}{|c|}f_{1} \\ f_{2} \\ \vdots \\ f_{n} \\ \end{array} = \overline {\begin{array}{|c|} f_{1} \\ f_{2} \\ \vdots \\ f_{n}\\ \end{array}} = \overline{f_{1}}.\overline{f_{2}} \ldots \overline{f_{n}} = (1 - f_{1}).(1-f_{2}) \ldots (1 - f_{n}) \]

Le complément d’un produel est égal au produit des compléments des facteurs duals qui le composent.

    \[ \overline{f_{1}.f_{2} \ldots f_{n}} s = \begin{array}{|c|} \overline{f_{1}} \\\overline{f_{2}} \\ \vdots \\ \overline{f_{1}} \\ \end{array} = 1 - (f_{1}.f_{2} \ldots f_{n}) \]

Le complément d’un produit est égal au produel des compléments des facteurs qui le composent.

Fonctions canoniques et tables de vérité

Toute fonction binaire peut s’exprimer soit par un produit de produels soit par un produel de produits. Les expressions obtenues sont appelées « fonctions canoniques ».

Si une fonction binaire dépend de « n » variables distinctes x_{1},x_{2}, \ldots x_{n}, nous ne pouvons envisager au total que 2^{n} combinaisons de valeurs distinctes (0 ou 1) de ces « n » variables. Si la fonction binaire est égale à l’unité pour « p » combinaisons, elle est nécessairement égale à zéro pour les « 2^n -p » combinaisons complémentaires et nous avons dans tous les cas p<2^n. Nous pouvons donc écrire la fonction sous la forme d’un produel de produits que nous appellerons, par définition, « première forme canonique ».

Nous appellerons « transposition », le passage, pour une même fonction, de la première à la deuxième forme canonique et réciproquement.

Établissement de la première forme canonique

On inscrit horizontalement les variables dans un ordre quelconque, puis on porte successivement sous ces variables dans le sens horizontal, les combinaisons de valeurs pour lesquelles la fonction est égale à l’unité. Il suffit alors de remplacer respectivement dans le tableau obtenu, chaque valeur « 1» par la variable « x_{k} » de la même colonne et chaque valeur « 0 » par le complément \overline{x_{k}} de la variable de la même colonne.

Exemple :

Établir la première forme canonique d’une fonction de trois variables x_{1}, x_{2}, x_{3}, égale à l’unité lorsqu’une des variables est égale à l’unité, les deux autres étant nulles.

La table de vérité s’écrit :

\begin{tabular}{|c|c|c||c|} \hline $x_{1}$ & $x_{2}$ & $x_{3}$ & $f$ \\ \hline 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 1 \\ \hline \end{tabular}

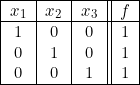
La première forme canonique s’établit immédiatement à partir de la table de vérité :

    \[ f = \begin{array}{|c|} x_{1} . \overline{x}_{2} . \overline{x}_{3} \\ \overline{x}_{1} . x_{2} . \overline{x}_{3} \\ \overline{x}_{1} . \overline{x}_{2} . x_{3} \\ \end{array} \]

Établissement de la deuxième forme canonique

Pour établir la deuxième forme canonique relative aux combinaisons de valeurs de « n » variables pour lesquelles cette fonction est nulle, on inscrit verticalement les variables x_{1}, x_{2},\ldots, x_{n} dans un ordre quelconque et successivement dans le même ordre vertical, les combinaisons de valeurs pour lesquelles f = 0. Il suffit alors d’écrire les produit des produels obtenus en remplaçant respectivement dans ce tableau, chaque valeur « 0 » par la variable « x_{k} » de la même ligne et chaque valeurs « 1 » — par le complément « \overline{x}_{k} » — de la variable de la même ligne.

Exemple :

Établir la deuxième forme canonique d’une fonction de trois variables x_{1}, x_{2}, x_{3}, égale à zéro lorsque deux au moins des trois variables sont égales à l’unité.

La table de vérité s’écrit :

\begin{tabular}{|c|c|c||c|} \hline $x_{1}$ &$x_{2}$ &$x_{3}$ & $f$ \\ \hline 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 0 \\ 1 & 1 & 0 & 0 \\ 1 & 1 & 1 & 0 \\ \hline \end{tabular}

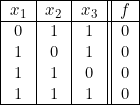
Comme nous l’avons indiqué précédemment, nous en tirons le tableau :

    \[ \begin{array} {c|c|c|c|c|} x_{1} & 0 & 1 & 1 & 1 \\ x_{2} & 1 & 0 & 1 & 1 \\ x_{3} & 1 & 1 & 0 & 1 \\ \end{array} \]

d’où la fonction cherchée :

    \[ f = \begin{array}{|c|c|c|c|} {x}_{1} &\overline{x}_{1} &\overline{x}_{1} &\overline{x}_{1} \\ \overline{x}_{2} &{x}_{2} &\overline{x}_{2} &\overline{x}_{2} \\ \overline{x}_{3} &\overline{x}_{3} &{x}_{3} &\overline{x}_{3} \\ \end{array} \]

Présentation des tables de vérité

Table de vérité complète.

Nous dirons qu’une table de vérité est complète lorsqu’elle fait apparaître la totalité des « 2^{n} » — combinaisons de valeurs possibles, relatives aux « n » — variables dont dépend la fonction.

Nous conviendrons d’inscrire les valeurs (0 ou 1) que prend la fonction à droite d’un double trait vertical de séparation et sur la même ligne que la combinaison correspondante des valeurs des variables.

Ainsi la table de vérité complète d’une fonction de trois variables, F(a, b, c), peut s’écrire par exemple :

  \begin{tabular}{r|c|c|c||c|} \multicolumn{1}{c} {} & \multicolumn{4}{c}{\it Table de vérité} \\ \cline{2-5} & a & b & c & F \\ \cline{2-5} 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 1 & 0 \\ 2 & 0 & 1 & 0 & 0 \\ 3 & 0 & 1 & 1 & 0 \\ 4 & 1 & 0 & 0 & 1 \\ 5 & 1 & 0 & 1 & 0 \\ 6 & 1 & 1 & 0 & 1 \\ 7 & 1 & 1 & 1 & 1 \\ \cline{2-5} \end{tabular}

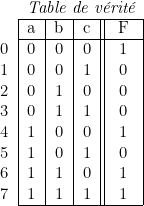
Il est souvent intéressant de faire figurer dans une colonne, à gauche, des repères décimaux qui correspondent aux nombres représentés par les chiffres binaires a, b, c, en plaçant ces nombres dans l’ordre naturel. Cette disposition permet, en particulier, de s’assurer qu’aucune combinaison n’a été oubliée.

Une table de vérité complète autorise, en suivant les règles énoncées précédemment, l’écriture immédiate de la fonction sous ses deux formes canoniques.

En ce qui concerne l’exemple donné, nous pouvons écrire :

    \[ F = \begin{array}{|c|} \overline{a} . \overline{b} . \overline{c}\\ {a} . \overline{b} . \overline{c}\\ {a} . {b} . \overline{c}\\ {a} . {b} . {c}\\ \end{array} = \begin{array}{|c|c|c|c|} a & a & a & \overline{a} \\ b & \overline{b} & \overline{b} & b \\ \overline{c} & c & \overline{c} & \overline{c} \\ \end{array} \]

La première forme utilise les combinaisons pour lesquelles F = 1, (0, 4, 6, 7), et la seconde forme les combinaisons pour lesquelles F = 0, (1, 2, 3, 5).

Tables de vérité incomplètes.

Une fonction binaire est entièrement définie si l’on connaît seulement les combinaisons de valeurs des variables pour lesquelles elle conserve la même valeur (0 ou 1).

Nous appellerons, par définition, table de vérité incomplète, le tableau dans lequel sont inscrites ces combinaisons. Nous préciserons, à droite de ce tableau, la valeur correspondante de la fonction. Pour chaque fonction il existe donc deux tables de vérité incomplètes.

Les deux tables de vérité incomplètes qui correspondent à la fonction précédente F(a, b, c) peuvent s’écrire suivant que l’on choisit pour « F » la valeur « 0 » ou la valeur « 1 » :

\begin{tabular}{l@{\hspace*{3cm}}r} \begin{tabular}{r|c|c|c||c|} \multicolumn{1}{c} {} & \multicolumn{4}{c}{{\it Table de vérité} ($F=1$)} \\ \cline{2-5} & a & b & c & F \\ \cline{2-5} 0 & 0 & 0 & 0 & \multirow{4}{*}{$F=1$} \\ 4 & 1 & 0 & 0 & \\ 6 & 1 & 1 & 0 & \\ 7 & 1 & 1 & 1 & \\ \cline{2-5} \end{tabular} & \begin{tabular}{r|c|c|c||c|} \multicolumn{1}{c} {} & \multicolumn{4}{c}{{\it Table de vérité} ($F=0$)} \\ \cline{2-5} & a & b & c & F \\ \cline{2-5} 1 & 0 & 0 & 1 & \multirow{4}{*}{$F=0$}\\ 2 & 0 & 1 & 0 & \\ 3 & 0 & 1 & 1 & \\ 5 & 1 & 0 & 1 & \\ \cline{2-5} \end{tabular} \end{tabular}

Une table de vérité incomplète ne permet d’écrire que l’une des deux formes canoniques. La propriété de dualité la rend cependant suffisante pour définir complétement une fonction binaire.

Tables de vérité réduites.

Ce sont des tables de vérité incomplète dans lesquelles certaines combinaisons sont groupées afin de tenir compte d’une partie ou de la totalité des adjacences qui existent entre elles. Ces adjacences étant repérées dans la table par le symbole « \phi » qui signifie que la valeur prise par la variable peut être indifféremment « 0 » ou « 1 ». Nous pouvons tirer de l’exemple pfécèdent différentes tables de vérités réduites, parmi lesquelles les deux suivantes :

\begin{tabular}{l@{\hspace*{3cm}}r} \begin{tabular}{r|c|c|c||c|} \cline{2-5} & a & b & c & F \\ \cline{2-5} 0-4 &$\phi$ & 0 & 0 & \multirow{2}{*}{$\big\rbrace F=1$} \\ 6-7 & 1 & 1 & $\phi$ & \\ \cline{2-5} \end{tabular} & \begin{tabular}{r|c|c|c||c|} \cline{2-5} & a & b & c & F \\ \cline{2-5} 1-5 & $\phi$ & 0 & 1 & \multirow{2}{*}{$\big\rbrace F=0$}\\ 2-3 & 0 & 1 & $\phi$ & \\ \cline{2-5} \end{tabular} \end{tabular}

L’adjacence, comme nous le verrons quand nous étudierons les simplifications, a pour effet de supprimer la variable biforme (directe et complémentée) dans le produit ou le produel qui résulte des combinaisons groupées. Une table de vérité réduite ne donne donc plus une forme canonique mais une forme déjà simplifiée. Dans le cas envisagé, nous tirons de la première table de vérité réduite :

    \[ F = \begin{array}{|c|} \overline{b} . \overline{c}\\ {a} . {b} \\ \end{array} \]

De la seconde table de vérité réduite nous tirons :

    \[ F = \begin{array}{|c|c|} {b} & {a} \\ \overline{c} & \overline{b}\\ \end{array} \]

Structures algébriques (bases)
 		Transformations
Page suivante