Notice B :
|
• Vous souhaitez connaître comment s’obtient un programme permettant de résoudre un problème, de jouer avec l’ordinateur J.R.01 ?
Vous avez raison ; c’est passionnant…
• Le but de cette notice est de vous indiquer comment concevoir, puis réaliser, un programme utilisable par le J. R. 01, de façon aussi simple et naturelle que possible, et sans le secours de la théorie mathématique.
• Pour cela, nous allons traiter complètement un exemple.
❶ Premier exemple
■ Considérons la situation suivante :
C’est l’été, je me promène. Une averse a mouillé la chaussée. Puis-je répondre à la seule question suivante : «dans quels cas me mouillerai-je ‘.3 » sachant que : il peut continuer de pleuvoir ou non ;si j’ai un para- pluie, j’admets qu’il m’abrite de la pluie ; si j’ai des chaussures aux pieds, j’admets que j’ai les pieds au sec.
■ Analyse du problème :
• Le problème comporte trois « informations » (ou « données ») :
- — « Il continue de pleuvoir ou non » ;
- — « j’ai un parapluie ou je n’en ai pas » ;
- — « j’ai des chaussures aux pieds ou je suis pieds nus ».
Nous pouvons convenir d’utiliser respectivement les barrettes A, B, C pour chacune des informations, et cela de la manière suivante :
- — Barrette A :
- — index sur la position 1, « il continue de pleuvoir »,
- — index sur la position 0, « il a cessé de pleuvoir » ;
- — Barrette B :
- — index sur la position 1, « j’ai un parapluie »,
- — index sur la position 0, « je n’ai pas de parapluie » ;
- — Barrette C :
- — index sur la position 1, « j’ai des chaussures aux pieds »,
- — index sur la position 0, « je suis nu pieds ».
• La solution du problème comporte une seule réponse, par oui ou non, à la question : « est-ce que je me mouille ? ». Une seule lampe (V, X, Y, ou Z) suffit donc pour donner cette réponse. convenons de choisir, par exemple, la lampe Y et posons la convention suivante :
- — lampe Y allumée, « je me mouille » ;
- — lampe Y éteinte, « je ne me mouille pas ».
Il reste à étudier-tous les cas possibles.
• Nombre de cas :
Puisqu’il y a, pour A, deux cas possibles (A sur 1 ou A sur 0, c’est-à-dire « il continue de pleuvoir» ou «il ne pleut plus ») et qu’il en est de même pour B, cela fait déjà 4 cas possibles. Or, de même, à chacun de ces
cas, C fait correspondre 2 cas. Par suite, l’étude du problème comporte 8 cas que des informations, et cela de la manière nous schématisons à l’aide du tableau ci-dessous :
| Index des barrettes sur : | A | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| B | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | |
| C | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
• Étude de tous les cas possibles :
- — Première colonne : A = 0, B = O, C = 0, c’est-à-dire « il ne pleut plus et je n’ai pas de parapluie et je n’ai pas de chaussures aux pieds ». Il est alors clair, la chaussée étant mouillée, que je me mouille les pieds, donc la lampe Y doit s’allumer.
- — Deuxième colonne : A = O, B = 0, C =1, c’est-à-dire «il ne pleut plus et je n’ai pas de parapluie et j’ai des chaussures aux pieds ». Dans ce cas, je ne me mouille pas ; la lampe Y doit rester éteinte.
- — Troisième colonne : A = 0, B = 1, C = O, c’est-à-dire « il ne pleut plus et j’ai un parapluie et je n’ai pas de chaussures aux pieds ». La chaussée étant mouillée, il est clair que… je me mouille les pieds. La lampe Y doit donc s’allumer.
- — Quatrième colonne : A = 0, B = 1, C = 1, c’est-à-dire « il ne pleut plus et j’ai un parapluie et j’ai des chaussures aux pieds ». Il en résulte que… je ne me mouille pas. Donc la lampe Y doit rester éteinte.
- — Cinquième colonne : A = 1, B = 0, C = 0, c’est—à-dire « il continue de pleuvoir et je n’ai pas de parapluie et je n’ai pas de chaussures aux pieds ». Il est alors certain… que je me mouille : donc la lampe Y doit s’allumer.
- — En procédant de même pour les sixième, septième et huitième colonne, on obtient le tableau ci-dessous (appelé table de valeurs) :
-
Index des barrettes sur : A 0 0 0 0 1 1 1 1 B 0 0 1 1 0 0 1 1 C 0 1 0 1 0 1 0 1 Sortie lampe Y Allumée Éteinte Allumée Éteinte Allumée Allumée Allumée Éteinte
Autrement dit, la lampe Y doit s’allumer dnas les cinq cas suivants (et seulement dans ces cas) :
- a) (colonne 1), l’index de la barrette A est placé sur 0, celui de la barrette B sur O et celui de la barrette C sur 0 ;
- b) (colonne 3), l’index de la barrette A est placé sur 0, celui de B sur 1 et celui de C sur 0 ;
- c) (colonne 5), l’index de la barrette A est sur 1, celui de B sur O et celui de C sur O ;
- d) (colonne 6), l’index de la barrette A est sur 1, celui de B sur O et celui de C sur 1 ;
- e) (colonne 7), l’index de la barrette A est sur 1, celui de B sur 1 et celui de C sur O.
■ Comment réaliser ce programme ?
- ① Du point de vue pratique, il faut savoir qu’une lampe s’allume (quand on appuie sur le bouton réponse) lorsque trois fiches se trouvent alignées sur une colonne de programmation (numérotées de 1 à 7 sur le pupitre du J.R.01) et que cette colonne est reliée à la lampe considérée.
Ainsi, si l’on se place dans le cas de la septième colonne du tableau ci-dessus (A :1, B = 1, C = 0), on doit obtenir le schéma indiqué figure 1. 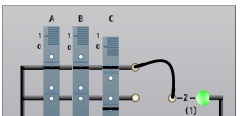
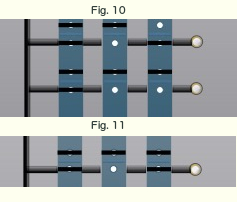
Règle 1 : pour une valeur 1 dans la table de valeurs, enfoncer une fiche dans le trou de gauche de la colonne de programmation ; pour une valeur 0, enfoncer une fiche dans le trou de droite.-
② Pour réaliser le programme correspondant à la table de valeur indiquée ci-dessus, nous devons donc choisir 5 colonnes de programmation (puisque la lampe Y doit s’allumer dans 5 cas) et les relier à la lampe Y.
Le choix des cinq colonnes est arbitraire.
Si nous choisissons les colonnes numérotées 1, 3, 5, 6, 7 pour représenter les cas indiqués, respectivement, dans les colonnes 1, 3, 5, 6, 7 de la table de valeurs, alors, en appliquant la règle 1 indiquée ci-dessus, nous obtenons le schéma du programme. A savoir :
③ Vérification du programme :
Si l’on place |’index de A sur 0, celui de B sur 0, celui de C sur 0 ; si l’on appuie sur le bouton réponse, la lampe Y doit s’allumer.
On vérifie ainsi successivement les 8 cas possibles indiqués par la table de valeurs.
|
❷ Comment simplifier un programme ?
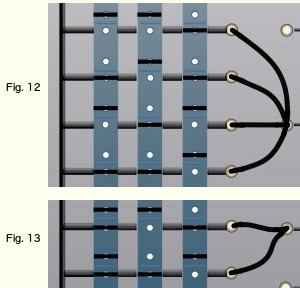
■ Pour traiter le simple exemple ci-dessus, il a été nécessaire d’utiliser 5 colonnes de programmation. Il est alors clair que, dans des problèmes plus complexes, les 7 colonnes du J.R.01 seraient vite insuffisantes, à moins que l’on simplifie le programme.■ Or, dans l’exemple traité, il est aisé de montrer que le programme indiqué figure 3 se simplifie en celui indiqué figure 4.(Pour vérifier cette affirmation il vous suffit de programmer l’ordinateur J. R. 01 comme indiqué figure 4 et de constater que la lampe Y s’allume effectivement dans les 5 cas prévus par la table de valeurs et reste éteinte dans les 3 autres cas).■ Règle de simplification : Si deux colonnes de programmation (reliées à la même lampe) présentent, sur |
Fig-4 |
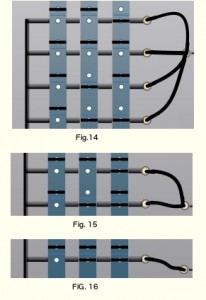
| b) Puisque la disposition des fiches est la même sur les barrettes A et C, il est possible de regrouper les colonnes de programmation 5 et 7, selon la seule colonne indiquée figure 6 ; |   Fig. 6 Fig. 6 |
  Fig. 7
Fig. 7 |
— La disposition des fiches étant, maintenant, la même sur les barrettes B et C (fig. 5 et 6) les deux colonnes de programmation obtenues se regroupent en une seule (fig. 7). |
— Ainsi, le programme indiqué figure 3 se réalise avec deux colonnes de programmation seulement à savoir : la colonne 6 inchangée et la colonne obtenue figure 7. Ceci conduit au programme indiqué figure 4, que nous avons réalisé en utilisant la colonne 2 de programmation à la place de la colonne 6 et la colonne 4 correspondant là la colonne obtenue figure 7 (et « condensant » les colonnes 1, 3, 5, 7). Bien entendu, deux autres colonnes auraient convenu.
❸ Deuxième exemple : Comment deviner le nombre choisi ? (voir notice 1)
■ Analyse du problème :
— Nous avons trois informations : les réponses par oui ou non aux trois questions posées. Chaque barrette A, B, C enregistrera donc une réponse (oui : index sur 1 ; non : index sur 0).
— La réponse est un nombre de 0 à 7. Pour l’obtenir, il faudra utiliser les trois lampes X, Y, Z. Ainsi par exemple :
—— (X éteinte, Y éteinte, Z éteinte) correspondra à 0 ;
—— X éteinte, Y éteinte, Z allumée) correspondra à 1 ;
— (X éteinte, Y allumée, Z éteinte) correspondra à 2 ;
— (X étejnte, Y allumée, Z allumée) correspondra à 3 ;
— (X allumée, Y éteinte, Z éteinte) correspondra à 4 ;
— (X allumée, Y éteinte, Z allumée) correspondra à 5 ;
— (X allumée, Y allumée, Z éteinte) correspondra à 6 ;
— (X allumée, Y allumée, Z allumée) correspondra à 7.
■ Table de valeurs :
— Si 0 est le nombre choisi, alors les réponses aux questions posées sont : <b>« oui »</b>, <b>« oui »</b>, <b>« oui »</b> ; c’est-à—dire correspondent à A = 1, B = 1, C = 1 (première colonne de la <b>Table</b>, ci-dessous).
| Index des barrettes sur : | A | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| B | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | |
| C | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | |
| Chiffres choisis : lampes | X | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| Y | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | |
| Z | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | |
| Nombre choisi en décimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
— Si 1 est le nombre choisi, alors les réponses « aux questions posées seront : « non », « oui », « oui » c’est-à-dire A=0, B = 1, C = 1.
—— En étudiant les huit cas possibles, on obtient la table de valeurs ci-dessous.
(À l’entrée : 1 = oui, O = non ; à la sortie : 1 = lampe allumée, 0 : lampe éteinte.
| ■ Programme : • La lampe X doit s’allumer dans 4 cas (à savoir les colonnes où le nombre choisi est 4, 5, 6 ou 7), ce qui, d’après la règle 1 correspond aux 4 colonnes de programmation indiquées ci-contre Fig. 9). |
Remarque
Si vous le souhaitez, il est possible, dans ce jeu, de remplacer la troisième question par
celle-ci : « Le nombre choisi est-il différent des nombres 0, 1, 6 et 7 ? » Si la réponse est
oui, mettre l’index de la barrette C sur 1 ; la mettre sur 0, dans le cas contraire.
Dans ce cas, il vous faut établir un nouveau programme en suivant les règles indiquées ci-dessus.
Ainsi est encore mis en évidence la grande variété d’utilisation du J.R.01.
❹ Si vous voulezvous « entraîner » à programmer, lisez, dans le livret 2 (à partir de la page 39) les parties « analyse du problème » et « Table de Valeurs » correspondant à toutes
les notices contenues dans le livret 1. Ensuite chercher à obtenir, en utilisant la règle de simplification, les programmes indiqués sur ces notices.
— Si vous désirez « comprendre » alors étudiez le livret 2.

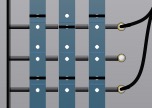

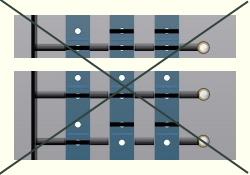
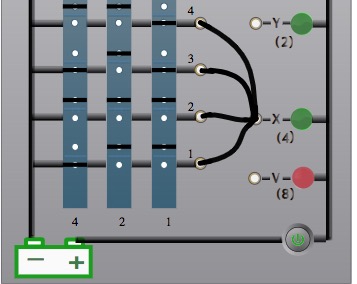 Fig. 9
Fig. 9