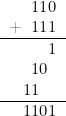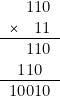Systèmes de numération

Le système binaire.

 00-Notice O
Page suivante

  • ➀ Le problème de la numération.

    Ce problème consiste à écrire et nommer tous les nombres entiers. Pour cela, il est nécessaire de posséder un nombre fini de symboles représentant certains d’entre eux et permettant d’obtenir tous les autres.

    Alors apparaissent deux contraintes contradictoires :

    • — si l’on a beaucoup de symboles initiaux, alors l’écriture (le codage) de tous les autres entiers sera simplifié mais il faut connaître une liste importante de « noms » et de « symboles » ;
    • — si l’on a peu de symboles initiaux, alors l’écriture (le codage) de tous les autres entiers sera longue.

    Ainsi dans la numération romaine,

    les symboles étaient : \begin{tabular}{ccccccc} \textsf{\mbox{I}} & \textsf{\mbox{V}} & \textsf{\mbox{X}} & \textsf{\mbox{L}} & \textsf{\mbox{C}} & \textsf{\mbox{D}} & \textsf{\mbox{M}}\\ {\bf un }& {\bf cinq} & {\bf dix} & {\bf cinquante} & {\bf cent} & {\bf cinq cents} & {\bf mille}\\ \end{tabular}

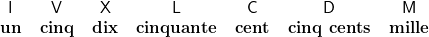
et les règles étaient :

  • 1° tout symbole placé immédiatement à droite d’un symbole supérieur s’ajoute à ce dernier :

    EXEMPLE : XVI seize ou DIX + CINQ + UN

  • 2° tout symbole placé immédiatement à gauche d’un symbole strictement supérieur se soustrait de ce dernier ;

    EXEMPLE : IX neuf ou DIX – UN

  • 3° tout symbole placé entre deux symboles strictement supérieur se retranche de celui de droite ;

    EXEMPLE : CIV cent quatre ou CENT + CINQ – UN

  • 4° les unités des classes supérieures sont soulignées une fois pour les mille, deux fois pour les millions, etc.

    EXEMPLE : \overline{\overline{\sc I}}\overline{\sc D} UN MILLION CINQ CENT MILLE.

Que de complications ! Imaginez effectuer une addition, une multiplication, une division avec deux entiers codés en numération romaine…

Un des inconvénients de la numération romaine apparaît immédiatement : un symbole représente toujours le même entier quelle que soit la place de ce symbole. Il en résulte qu’il faut utiliser la règle (4°) pour obtenir des « unités d’ordre supérieur ».

C’est pour éviter cet inconvénient que les numérations utilisées maintenant sont des numérations de position : cela signifie qu’un même symbole représente différents entiers suivant la place qu’il occupe dans l’écriture d’un nombre.

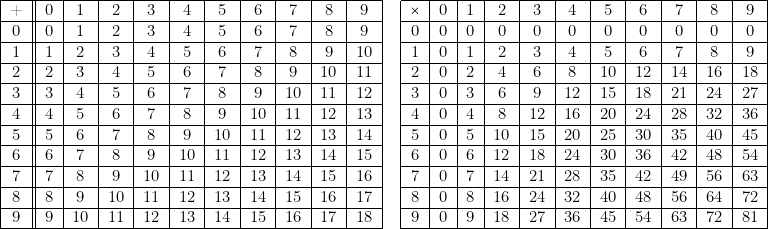
  • ➁ Numération décimale.

    Elle utilise dix symboles, appelés chiffres :

    \begin{tabular}{rrccccccccc} écrits & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9\\ lus & zéro & un & deux & trois & quatre & cinq & six & sept & huit & neuf\\ \end{tabular}

    • — Ensuite, l’entier suivant contient une dizaine et zéro unité.Il s’écrit donc 10 (lire dix). On obtient alors, successivement, 11 , 12…. 19.
    • — Après ? deux dizaines et zéro unité, soit 20 (lire vingt), etc…
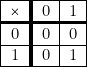
    • — Les « calculs » s’effectuent à l’aide des tables d’addition et de multiplication ci-dessous (la somme a + b ou le produit a \times b s’obtiennent à l’intersection de la colonne de a avec la ligne de b).

    \begin{tabular}{|c||c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \cline{1-11} \cline{13-23} + & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & & $\times$ & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9\\ \cline{1-11} \cline{13-23} 0 & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ \cline{1-11} \cline{13-23} 1 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & & 1 & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9\\ \cline{1-11} \cline{13-23} 2 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & & 2 & 0 & 2 & 4 & 6 & 8 & 10 & 12 & 14 & 16 & 18\\ \cline{1-11} \cline{13-23} 3 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & & 3 & 0 & 3 & 6 & 9 & 12 & 15 & 18 & 21 & 24 & 27\\ \cline{1-11} \cline{13-23} 4 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & & 4 & 0 & 4 & 8 & 12 & 16 & 20 & 24 & 28 & 32 & 36\\ \cline{1-11} \cline{13-23} 5 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & & 5 & 0 & 5 & 10 & 15 & 20 & 25 & 30 & 35 & 40 & 45\\ \cline{1-11} \cline{13-23} 6 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & & 6 & 0 & 6 & 12 & 18 & 24 & 30 & 36 & 42 & 48 & 54\\ \cline{1-11} \cline{13-23} 7 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16 & & 7 & 0 & 7 & 14 & 21 & 28 & 35 & 42 & 49 & 56 & 63\\ \cline{1-11} \cline{13-23} 8 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16 & 17 & & 8 & 0 & 8 & 16 & 24 & 32 & 40 & 48 & 56 & 64 & 72\\ \cline{1-11} \cline{13-23} 9 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16 & 17 & 18 & & 9 & 0 & 9 & 18 & 27 & 36 & 45 & 54 & 63 & 72 & 81\\ \cline{1-11} \cline{13-23} \end{tabular}

  • ➂ Numération binaire.
    • 1° Écriture d’un entier. Elle utilise deux symboles (chiffres) notés 0, 1 (lus « zéro » et « un »).

        Ensuite : deux est formé d’une paire et de zéro unité. Il est donc codé 10 (lire « un, zéro » ; trois est formé d’une paire et une unité. « est donc codé 11 (lire « un, un »).
      • On obtient donc la correspondance suivante :

      \begin{tabular}{rcrl} \multicolumn{1}{c}{ {\bf Système décimal}} & & \multicolumn{2}{c}{ {\bf Système binaire}}\\ 0 & & 0 & \\ 1 & & 1 & \\ 1 & & 10 & \\ 3 & & 11 & \\ 4 & & 100 & (lire {\bf « un, zéro, zéro »})\\ 5 & & 101 & \\ 6 & & 110 & \\ 7 & & 111 & \\ 8 & & 1000 & \\ 9 & & 1001 & (lire {\bf « un, zéro, zéro, un »})\\ \end{tabular}

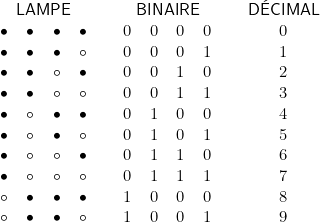
      Remarque Un entier s’écrira simplement en système binaire à l’aide de lampes allumées (pour 1) ou éteintes (pour zéro). Ainsi, avec quatre lampes, on pourra écrire les nombres suivants (rond noir : lampe éteinte ; rond blanc : lampe allumée).

      \begin{tabular}{ccccccccccc} \multicolumn{4}{c}{\textsf{LAMPE}} & & \multicolumn{4}{c}{\textsf{BINAIRE}} & & \textsf{DÉCIMAL}\\ $\bullet$ & $\bullet$ & $\bullet$ & $\bullet$ & & 0 & 0 & 0 & 0 & & 0\\ $\bullet$ & $\bullet$ & $\bullet$ & $\circ$ & & 0 & 0 & 0 & 1 & & 1\\ $\bullet$ & $\bullet$ & $\circ$ & $\bullet$ & & 0 & 0 & 1 & 0 & & 2\\ $\bullet$ & $\bullet$ & $\circ$ & $\circ$ & & 0 & 0 & 1 & 1 & & 3\\ $\bullet$ & $\circ$ & $\bullet$ & $\bullet$ & & 0 & 1 & 0 & 0 & & 4\\ $\bullet$ & $\circ$ & $\bullet$ & $\circ$ & & 0 & 1 & 0 & 1 & & 5\\ $\bullet$ & $\circ$ & $\circ$ & $\bullet$ & & 0 & 1 & 1 & 0 & & 6\\ $\bullet$ & $\circ$ & $\circ$ & $\circ$ & & 0 & 1 & 1 & 1 & & 7\\ $\circ$ & $\bullet$ & $\bullet$ & $\bullet$ & & 1 & 0 & 0 & 0 & & 8\\ $\circ$ & $\bullet$ & $\bullet$ & $\circ$ & & 1 & 0 & 0 & 1 & & 9\\ \end{tabular}

    • 2° Addition
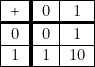
      La table d’addition est d’une simplicité extrême, puisque : 0+0=0 \qquad 1 + 0 = 0 \qquad 0 +1=1, et 1+1=10 Par suite, toutes les additions d’entiers écrits en système binaire sont d’une extrême simplicité (on commence toujours par les chiffres de droite).

      Exemple : 110 +111 = ? \begin{tabular}{c@{}r@{}c@{}c@{}c} && 1 & 1 & 0 \\ \multicolumn{2}{l}{+} &1 & 1 & 1 \\ \hline && & & 1 \\ && 1 & 0 & \\ &1 & 1 & & \\ \hline &1& 1 & 0 & 1\\ \end{tabular} \begin{tabular}{|c|@{\vrule width 1.5pt}|c|c|} \hline $\displaystyle \mathbf{ + }$ & 0 & 1\\ \Mline 0 & 0 & 1\\ \hline 1 & 1 & 10\\ \hline \end{tabular}
      d’où 110 + 111 = 1101
    • 3° Multiplication

    En système binaire, les multiplications sont d’une simplicité exemplaire puisque la table de multiplication se réduit à : 0\times 0=0 \qquad 1 \times 0 = 0 \qquad 0 \times 1=0, et 1\times 1=1 La disposition pratique pour effectuer une multiplication est, bien sûr, la même que dans le système décimal.

    Exemple : 110 \times 11 = ? \begin{tabular}{c@{}c@{}c@{}c@{}c} && 1 & 1 & 0 \\ \multicolumn{3}{l}{$\times$ } & 1 & 1 \\ \hline &&1 &1 & 0 \\ &1&1 & 0 & \\ \hline 1& 0& 0 & 1&0\\ \end{tabular} \begin{tabular}{|c|@{\vrule width 1.5pt}|c|c|} \hline $\mathbf{\times }$ & 0 & 1\\ \Mline 0 & 0 & 0\\ \hline 1 & 0 & 1\\ \hline \end{tabular}
    d’où 110 \times 11 = 10010
  • 4° Comment coder en numération décimale un nombre écrit en numération binaire ? Soit, par exemple, a = 11101. Cela signifie a = 10000 + 1000 + 100+ 1 Or, d’après ce qui précède, 10 \rightarrow 2 \qquad 100 \rightarrow 4=2^2 \qquad 1000 \rightarrow 8= 2^3 \qquad 10000 \rightarrow 16 = 2^4 Par suite, a=16+8+4+1, soit a=29 Autrement dit, il suffit de connaître les puissances successives de deux. C’est pour cela que le système binaire est aussi appelé système base deux.
  • Remarque : Le système décimal est à base dix.
    En effet, si b = 1971 cela signifie
    b= 1000 + 9 \times 100 + 7\times 10 + 1
    soit b= 10^3 + 9\times 10^2 + 7 \times 10 + 1
  • 5° Problème inverse : Comment écrire en système binaire un nombre écrit en base dix ? D’après ce qui précède, il suffit de le décomposer en une somme de puissances de 2. Pour cela, il suffit, pratiquement de diviser le nombre donné par 2 (pour obtenir le nombre de paires),le reste donne le nombre d’unités restantes ;

    • — puis diviser le quotient obtenu par 2 (pour obtenir le nombre de « quadrilles »), le reste donnera le nombre de paires restantes ;
    • — puis le quotient obtenu sera divisé encore par 2 (pour obtenir le nombre (d’octaves »), le reste donnera le nombre de « quadrilles » restants ; etc…

    • Exemple : Écrire 47 en base deux.

    1e méthode : 47 = 32+8 +4 +2 + 1
    donc, = 1\quad 0 \quad 1 \quad 1 \quad 1 \quad 1
    (car il n’y a pas 16 = 2^4 )
    2e méthode : 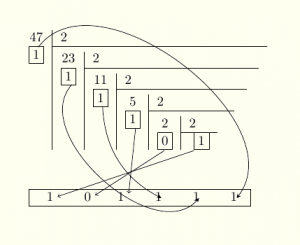Conversion_47_base_2

    Remarque : On peut « vérifier », dans le système décimal, les opérations effectuées ci-dessus dans le système binaire (page précédente).

    — Addition 110 + 111
    En décimal : 110 \longrightarrow 6 \qquad 111 \longrightarrow 7
    Or 6+7= 13 et 13 = 8+4+ 1
    = 2^3 + 2^2 + 1
    et 13 \longrightarrow 1101
    — Multiplication 110 \times 11
    En décimal : 110 \longrightarrow 6 \qquad 11 \longrightarrow 3
    Or 6\times3= 18 et 18 = 16+2
    = 2^4 + 2
    et 18 \longrightarrow 10010
    (il « manque » 2^3, 2^2 et il n’y a pas d’unité)

    6° Et l’ordinateur J.R. 01 ?

    Bien qu’il ne soit pas un « calculateur » rapide (l’introduction des données, à l’entrée, se faisant « à la main »), le J. R. 01 est capable d’effectuer des additions et des multiplications.

    – Pour une addition de deux nombres, on les écrit en système binaire, on programme l’ordinateur J.R. 01 comme indiqué ci-dessous, on introduit le dernier chiffre, de droite, (0 ou 1) du premier nombre à l’aide de la barrette B, celui du deuxième nombre à l’aide de la barrette C. La lampe X allumée donnera 1, éteinte O. On écrit le chiffre indiqué. C’est le dernier chiffre de droite de la somme. La lampe Z allumée indique qu’il faut reporter 1 à l’aide de la barrette A. On recommence… C’est-à-dire qu’on introduit les chiffres suivants des nombres à additionner. Et le processus se poursuit…

    Z (à reporter en A)
     

     

    — Pour une multiplication, on revient à une addition en confiant à l’ordinateur J.R. 01 le soin de faire les totaux des produits partiels (110 + 1100 dans l’exemple ci-dessus).

    Systèmes de numération
         		00-Notice O
    Page suivante